Пусть при этом , тогда, возведя в квадрат обе части равенства, получим
не удовлетворяет условию при |t|≤√2
Возвращаемся к обратной замене
Пусть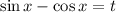 при этом
при этом 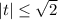 , тогда, возведя в квадрат обе части равенства, получим
, тогда, возведя в квадрат обе части равенства, получим 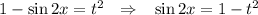
Возвращаемся к обратной замене