{}
Объяснение:
Выберем корни, принадлежащие отрезку [ 0; 2π]
1) при n=0, x=0;
при n=1, x=π;
при n=2, x=2π.
2) при k=0, x= .
Объяснение:
Выберем корни, принадлежащие отрезку [ 0; 2π]
1) при n=0, x=0;
при n=1, x=π;
при n=2, x=2π.
2) при k=0, x=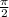 .
.