Объяснение:
1)
а )25а⁴с⁶:(-27а⁹с⁶)=-
б) 2а-3а²-а²+2а-1=-4а²+4а-1
в)
2)
a) 10-2x-2x=x-25
10-4x=x-25
-5x=-35
x=7
б) домножим на 6, чтобы избавитьсяот знаменателя
2(3х+2)=3(х-4)
6х+4=3х-12
3х=-16
х=-5
в) х²=4
х₁=2; х₂=-2
3) 36-(3m+2n)²
4) из первого уравнения у=2х+3
3х-2(2х+3)=7
3х-4х-6=7
-х=13
х=-13
у=-13*2+3=-23
5)
6) В - самый маленький угол - х
угол А=2х
угол С=6х
х+2х+6х=180
9х=180
х=20 = угол В
40 - угол А
120 - угол С
вариант 2
1) а) 9m⁴n⁶:(-8m⁹n⁶)=
б) 2x-x²-x²+2x-1=4x-2x²-1
2) 3x+6-2x=8-x
2x=2
x=1
б,)умножим на 20,чтоб избавиться от знаменателя
4(2х+3)=5(4-х)
8х+12=20-5х
13х=8
х=
в) х²=9
х1=3; х2=-3
3) 25-(2m-n)²=(5-2m+n)(5+2m-n)
4) из второго у=3х-2
2х+3(3х-2)=5
2х+9х-6=5
11х=11
х=1
у=3-2=1
при х=2 1/9*8=
6) угол В=х
Угол А=3х
х+3х+6х=180
10х=180
угол В=18
угол А=54
угол С=108
-3.
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
Объяснение:
1)
а )25а⁴с⁶:(-27а⁹с⁶)=-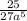
б) 2а-3а²-а²+2а-1=-4а²+4а-1
в)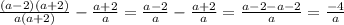
2)
a) 10-2x-2x=x-25
10-4x=x-25
-5x=-35
x=7
б) домножим на 6, чтобы избавитьсяот знаменателя
2(3х+2)=3(х-4)
6х+4=3х-12
3х=-16
х=-5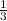
в) х²=4
х₁=2; х₂=-2
3) 36-(3m+2n)²
4) из первого уравнения у=2х+3
3х-2(2х+3)=7
3х-4х-6=7
-х=13
х=-13
у=-13*2+3=-23
5)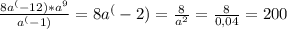
6) В - самый маленький угол - х
угол А=2х
угол С=6х
х+2х+6х=180
9х=180
х=20 = угол В
40 - угол А
120 - угол С
вариант 2
1) а) 9m⁴n⁶:(-8m⁹n⁶)=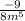
б) 2x-x²-x²+2x-1=4x-2x²-1
в)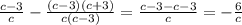
2) 3x+6-2x=8-x
2x=2
x=1
б,)умножим на 20,чтоб избавиться от знаменателя
4(2х+3)=5(4-х)
8х+12=20-5х
13х=8
х=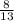
в) х²=9
х1=3; х2=-3
3) 25-(2m-n)²=(5-2m+n)(5+2m-n)
4) из второго у=3х-2
2х+3(3х-2)=5
2х+9х-6=5
11х=11
х=1
у=3-2=1
5)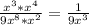
при х=2 1/9*8=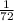
6) угол В=х
Угол А=3х
угол С=6х
х+3х+6х=180
10х=180
угол В=18
угол А=54
угол С=108
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.