Розкласти у вигляді добутку 1/27a^12b18+64c^9 - вопрос №127121864916629826 от Аnuk 20.08.2022 04:45

Question

Алгебра: Розкласти у вигляді добутку 1/27a^12b18+64c^9

Аnuk · Answer

1) не является; 2) не является; 3) не является

Объяснение:

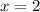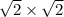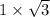
1) Рассмотрим x=2 . Заметим, что такая диагональ есть у прямоугольников с размерами $\sqrt{2}\times\sqrt{2}$ и $1\times\sqrt{3}$

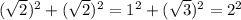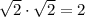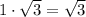( $(\sqrt{2})^2+(\sqrt{2})^2=1^2+(\sqrt{3})^2=2^2$ ), при этом их площади равны $\sqrt{2}\cdot \sqrt{2}=2$ и $1\cdot \sqrt{3}=\sqrt{3}$ соответственно.

Значит, y не является функцией x.

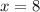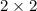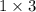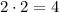2) Рассмотрим x=8 . Заметим, что такой периметр есть у прямоугольников с размерами $2\times2$ и $1\times3$ , при этом их площади равны $2\cdot 2=4$ и $1\cdot 3=3$ соответственно.

Значит, y не является функцией x.

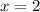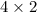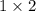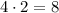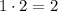3) Рассмотрим x=2 . Заметим, что такая диагональ есть у прямоугольников с размерами $4\times2$ и $1\times2$ , при этом их площади равны $4\cdot 2=8$ и $1\cdot 2=2$ соответственно.

Значит, y не является функцией x.