Пусть 2-я труба наполняет бассейн за х часов, тогда 1-я труба наполняет бассейно за (х -18) часов. Производительность (работа за 1 час) 1-й трубы: 1/(х -18), 2-й трубы: 1/х. Их общая производительность: 1/(х -18) + 1/х.
Работая вместе, они сделали всю работу (равную 1) за 12 часов
Уравнение:
(1/(х -18) + 1/х)·12 = 1
12·(х + х - 18) = х² - 18х
х² - 42х + 216 = 0
D = 42² - 4·216 = 900
√D = 30
х₁ = (42 - 30) : 2 = 6 (не подходит по условию задачи, даже работая вместе трубы наполняют бассейн за 12 часов!)
Пусть 2-я труба наполняет бассейн за х часов, тогда 1-я труба наполняет бассейно за (х -18) часов. Производительность (работа за 1 час) 1-й трубы: 1/(х -18), 2-й трубы: 1/х. Их общая производительность: 1/(х -18) + 1/х.
Работая вместе, они сделали всю работу (равную 1) за 12 часов
Уравнение:
(1/(х -18) + 1/х)·12 = 1
12·(х + х - 18) = х² - 18х
х² - 42х + 216 = 0
D = 42² - 4·216 = 900
√D = 30
х₁ = (42 - 30) : 2 = 6 (не подходит по условию задачи, даже работая вместе трубы наполняют бассейн за 12 часов!)
х₂ = (42 + 30) : 2 = 36
ответ: 2-я труба наполняет бассейн за 36 часов
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е.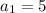 .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е.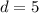 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.