Задание 2. Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 390 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 685 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?
Решение.
Пусть х руб. - стоит один детский билет.
По условию 2 детских билета и один взрослый стоят 390 рублей, значит,
(390-2х) руб. - стоит один взрослый билет.
Ещё в условии сказано, что 3 детских билета и 2 взрослых стоят всего 685 рублей.
Задание 1.
ответ: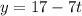
или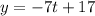
Задание 2. Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 390 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 685 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?
Решение.
Пусть х руб. - стоит один детский билет.
По условию 2 детских билета и один взрослый стоят 390 рублей, значит,
(390-2х) руб. - стоит один взрослый билет.
Ещё в условии сказано, что 3 детских билета и 2 взрослых стоят всего 685 рублей.
Получаем уравнение:
3х + 2 · (390-2х) = 685
3х + 780 - 4х = 685
-х = - 95
х = - 95 : (-1)
х = 95 руб. - стоит один детский билет.
390-2·95=200 руб. - стоит один взрослый билет.
Детский билет стоит 95 рублей,
а взрослый билет стоит 200 рублей.
x² - y² = 12
(x - y)(x + y) = 12
x-y x+y целые
12 = 2*2*3
Составляем пары , которыми могут быть значения
(1, 12) (12,1) (-1, -12) (-12, -1)
(2, 6) (6, 2) (-2, -6) (-6, -2)
(3, 4) (4, 3) (-3, -4) (-4, -3)
Составляем 12 систем
x + y = 1
x - y = 12
x + y = 12
x - y = 1
x + y = -1
x - y = -12
---
x + y = -12
x - y = -1
2x = 13 x = 6.5 нет значения не целые
оставляем где значения четные
x + y = 2 2x = 8 x = 4
x - y = 6 y = -2
x + y = 6 2x = 8 x = 4
x - y = 2 y = 2
x + y = -2 2x = -8 x = -4
x - y = -6 y = 2
---
x + y = -6 2x = -8 x = -4
x - y = -2 y = -2
ответ (4, 2) (4, -2) (-4, -2) (-4, 2)