Розв’яжіть систему нерівностей: -5<(-1-3х)/2<2 (х+1)/3 - (х-1) /2 <1​

1) 2x⁶y³ - ln7y*ln8x=0;

(2x⁶y³ - ln7y*ln8x)'=0;

12x⁵y³ + 2x⁶·3y²·y' - (1/7y)·7y'·ln8x - ln7y·(1/8x)·8 = 0;

12x⁵y³ + 6x⁶y²·y' - (y'ln8x)/y - ln7y·(1/x) = 0;

12x⁵y³ + y'(6x⁶y² - (ln8x)/y) - ln7y·(1/x) = 0;

y'(6x⁶y² - (ln8x)/y) = ln7y/x - 12x⁵y³;

y' = (ln7y/x - 12x⁵y³)/(6x⁶y² - (ln8x)/y).

2) y=(5x²+6)^arctg8x;

lny = arctg8x·ln(5x²+6);

(lny)' = (arctg8x·ln(5x²+6))';

y'/y = (8/(1+64x²))·ln(5x²+6) + (10x·arctg8x)/(5x²+6);

y' = y((8/(1+64x²))·ln(5x²+6) + (10x·arctg8x)/(5x²+6));

y' = ((5x^2+6)^arctg8x)·((8/(1+64x²))·ln(5x²+6) + (10x·arctg8x)/(5x²+6));

Решим дискриминант и решим методом интервала неравенство:

x²+2x-3=0

a=1 b=2 c=-3

D = b²-4ac => 2²-4*1*(-3) = 4+12 = 16>0, 2 корня.

√16 = 4

x = \frac{-b+-\sqrt{D} }{2a

x₁ =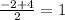

x₂ =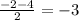

Получаем: (x-1)(x+3)>0, то есть x=-3 и x=1, нанесём на луч.

-----------------0--------------------0------------>

                  -3                        1              x

Научу методу интервала: превращаем сначала наше полученное выражение в уравнение: (x-1)(x+3)=0

Подставим число 2: f(2) = (2-1)(2+3) = 1*6 = 6, значит число положительное, ставим плюс в самом правом интервале.

Теперь, отталкиваясь от того, что плюс в самой правой части интервала, идём последовательно: + - +. Где плюсы - это и есть наш ответ, минус - неа, не ответ.

-∞                                                    +∞

\\\\\\\\\\\\\0--------------------0//////////>

             -3                        1           x

ответ: (-∞;-3)∪(1;+∞).