одз: х≠3; х≠ –3
2a²–(x+3)a–x²+3x=0;
x²+(a–3)x–2a²+3a=0
d=(a–3)²–4(–2a²+3a)=a²–6a+9+8a²–12a=9(a–1)²
если d=0 квадратное уравнение имеет один корень
d=0 при х=1
уравнение принимает вид
х²–2х+1=0 и имеет единственный корень х=1
при d≠0
уравнение имеет два корня
х₁=(–а+3+3а–3)/2=а х₂=(–а–3–3а+3)/2=–2а+3
если один из этих корней равен 3 или –3, т.е не входит в одз, тогда уравнение будет иметь единственный корень
если х₁=а=3, то х₂=–2а+3 = –3.
уравнение не имеет корней.
если х₁=а= –3 ,то есть а=–3, х₂=–2а+3 = 9.
уравнение имеет единственный корень.
если х₂=3, то есть –2а+3=3, то а=0.
уравнение имеет единственный корень х₁=а=0
случай х₂= –3 рассмотрен выше.
о т в е т при а=0; а=1; а=–3 уравнение имеет единственный корень
16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на дороже. то есть цена этого товара стала
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16
одз: х≠3; х≠ –3
2a²–(x+3)a–x²+3x=0;
x²+(a–3)x–2a²+3a=0
d=(a–3)²–4(–2a²+3a)=a²–6a+9+8a²–12a=9(a–1)²
если d=0 квадратное уравнение имеет один корень
d=0 при х=1
уравнение принимает вид
х²–2х+1=0 и имеет единственный корень х=1
при d≠0
уравнение имеет два корня
х₁=(–а+3+3а–3)/2=а х₂=(–а–3–3а+3)/2=–2а+3
если один из этих корней равен 3 или –3, т.е не входит в одз, тогда уравнение будет иметь единственный корень
если х₁=а=3, то х₂=–2а+3 = –3.
уравнение не имеет корней.
если х₁=а= –3 ,то есть а=–3, х₂=–2а+3 = 9.
уравнение имеет единственный корень.
если х₂=3, то есть –2а+3=3, то а=0.
уравнение имеет единственный корень х₁=а=0
случай х₂= –3 рассмотрен выше.
о т в е т при а=0; а=1; а=–3 уравнение имеет единственный корень
16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на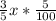
дороже. то есть цена этого товара стала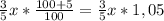 
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила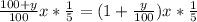
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16