1) Является ли у функцией х, если у - это число десятых в десятичной записи числа х?
У некоторых чисел существует 2 формы десятичной записи: с 0 и с 9 в периоде.
Например, для числа 1 существуют 2 формы: и . В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной , которому соответствуют несколько значений .
Значит, у не является функцией х.
2) Является ли x функцией y, если у - это число десятых в десятичной записи числа х?
Рассмотрим . Но число десятых у чисел и равно нулю. То есть существует значение переменной , которому соответствуют несколько значений (например, ).
R(р)>240000-наибольшая цена r(p)=q×p-выручка q×p>240000 q×p>240 q=100-10p (100-10p)p>240 100p-10p²>240 10p²-100p+240<0 р^2-10p+24<0 Квадратное уравнение p2 - 10p + 24=0 имеет два корня: p=4 и p=6. Следовательно, используя метод интервалов, решение неравенства будет интервал [4,6].Значит, наибольшая цена товара, позволяющая получить ежемесячную выручку не менее 240 000 рублей - 6 тысяч рублей.ответ: наибольшая цена, позволяющая предприятию получить необходимую выручку – 6 тыс. рублей.
1) не является; 2) не является
Объяснение:
1) Является ли у функцией х, если у - это число десятых в десятичной записи числа х?
У некоторых чисел существует 2 формы десятичной записи: с 0 и с 9 в периоде.
Например, для числа 1 существуют 2 формы: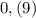
и 
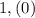. В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной 
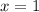, которому соответствуют несколько значений 
.
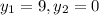Значит, у не является функцией х.
2) Является ли x функцией y, если у - это число десятых в десятичной записи числа х?
Рассмотрим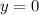
. Но число десятых у чисел 
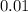и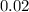 
равно нулю. То есть существует значение переменной 
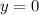, которому соответствуют несколько значений 
(например,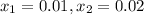 
).
Значит, x не является функцией y.
r(p)=q×p-выручка
q×p>240000
q×p>240
q=100-10p
(100-10p)p>240
100p-10p²>240
10p²-100p+240<0
р^2-10p+24<0
Квадратное уравнение p2 - 10p + 24=0 имеет два корня: p=4 и p=6. Следовательно, используя метод интервалов, решение неравенства будет интервал [4,6].Значит, наибольшая цена товара, позволяющая получить ежемесячную выручку не менее 240 000 рублей - 6 тысяч рублей.ответ: наибольшая цена, позволяющая предприятию получить необходимую выручку – 6 тыс. рублей.