Пусть медведь весит х кг.
1. За зиму медведь похудел на 20%, то есть на 0,20*х=0,2х кг. Его вес стал равен х-0,2х=0,8х кг.
2. Потом медведь поправился на 10%, то есть на 0,10*(0,8х)=0,08х кг. Его вес стал равен 0,8х+0,08х=0,88х кг.
3. Затем медведь опять похудел на 10%, то есть на 0,10*(0,88х)=0,088х кг. Его вес стал равен 0,88х-0,088х=0,792х кг.
4. Далее медведь поправился на 20%, то есть на 0,20*0,792х=0,1584х кг. Его вес стал равен 0,792х+0,1584х=0,9504х кг
5. Вес медведя стал меньше по сравнению с первоначальным на х-0,9504х=0,0496х кг, то есть вес стал на 0,0496*100%=4,96% меньше первоначального.
Замечание. Чтобы найти 10% , то есть от числа А, надо . Чтобы найти 20%, то есть от числа А, надо .
Пусть медведь весит х кг.
1. За зиму медведь похудел на 20%, то есть на 0,20*х=0,2х кг. Его вес стал равен х-0,2х=0,8х кг.
2. Потом медведь поправился на 10%, то есть на 0,10*(0,8х)=0,08х кг. Его вес стал равен 0,8х+0,08х=0,88х кг.
3. Затем медведь опять похудел на 10%, то есть на 0,10*(0,88х)=0,088х кг. Его вес стал равен 0,88х-0,088х=0,792х кг.
4. Далее медведь поправился на 20%, то есть на 0,20*0,792х=0,1584х кг. Его вес стал равен 0,792х+0,1584х=0,9504х кг
5. Вес медведя стал меньше по сравнению с первоначальным на х-0,9504х=0,0496х кг, то есть вес стал на 0,0496*100%=4,96% меньше первоначального.
Замечание. Чтобы найти 10% , то есть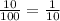 от числа А, надо
от числа А, надо 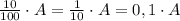 . Чтобы найти 20%, то есть
. Чтобы найти 20%, то есть 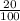 от числа А, надо
от числа А, надо 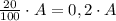 .
.
Уравнение имеет два различных корня при D > 0.
D = b^2 - 4ac = (2(a - 1))^2 - 4*(a^2 - 1)*2 = 4a^2 - 8a + 4 - 8a^2 + 8 =
= -4a^2 - 8a + 12 = -4(a^2 + 2a - 3)
D > 0 > -4(a^2 + 2a - 3) > 0
a^2 + 2a - 3 < 0
a^2 + 2a - 3 = 0
По теореме Виета а_1 = -3, а_2 = 1
Решением неравенства D > 0 , будет -3 < a < 1
ответ. (-3; 1)