С—9. Построение графика квадратичной
функции
1. Найдите координаты вершины параболы:
а) g(x) = х2 + 4х + 2;
б) g(x) = -х2 – 6х + 3;
В) 8 (x) = 4х2 – 8x - 1.
При вычислении воспользуйтесь формулами т =-
2а
b
и
b
n =g
2а
где тип – координаты вершины параболы
g(x) = ах2 + bx + c.
2. Используя результаты вычислений в задании 1а, по-
стройте график функции g(x) = х2 + 4х + 2. Найдите по
графику:
а) нули функции; промежутки,
в которых g(x) < 0 и
g(x) > 0;
б) промежутки убывания и возрастания функции; най-
меньшее ее значение.
40 вариант 2
ответ: 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
Объяснение:
Запишем данный многочлен в виде 2*(x³+5/2*x²+1/2*x-1). Для того, чтобы разложить многочлен в скобках на множители, нужно решить уравнение x³+5/2*x²+1/2*x-1=0. Это - приведённое кубическое уравнение, поэтому одним из его целых корней (если они есть) может быть целый делитель свободного члена данного уравнения, то есть числа -1. Таких делителей всего два: 1 и -1. Подставляя значения x=1 и x=-1 в данное уравнение, находим, что число x=1 не является корнем уравнения, а число x=-1 - является. Теперь разделим многочлен x³+5/2*x²+1/2*x-1 на двучлен x-(-1)=x+1. После этого получим тождество x³+5/2*x²+1/2*x-1=(x+1)*(x²+3/2*x-1). Теперь разложим на множители квадратный трёхчлен x²+3/2*x-1, для чего нужно решить уравнение x²+3/2*x-1=0. Оно имеет корни x1=1/2 и x2=-2, поэтому x²+3/2*x-1=0=(x-1/2)*(x+2). Тогда x³+5/2*x²+1/2*x-1=(x+1)*(x-1/2)*(x+2) и окончательно 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
27 км/год
6 км/год
Объяснение:
Возьмем за x - власну швидкість
Проти течії: S = 4 ; V = x - Vтеч; T= Tпр.т.
За течією: S = 15 ; V = x + Vтеч; T= Tза.т.
Без течії: S=18; V=x; T= Tпр.т.+Tза.т.
Формулы: S=V*T; V=S/T; T=S/V
Tпр.т.= 4/(x - Vтеч), за умовою: Vтеч = 3 км/год.
Tпр.т.= 4/(x - 3)
Tза.т.=15/(x+3)
T(без течії)=18/x, а також:
T(без течії)=Tпр.т.+Tза.т
Тому можемо зробити рівняння:
Tпр.т.+Tза.т=18/x
4/(x - 3) + 15/(x+3) = 18/x
(4x+12+15x-45)x = 18(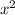 - 9)
- 9)
19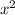 -33x-18
-33x-18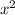 +152=0
+152=0
D=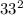 -4*162=441
-4*162=441
x1=(33+21)/2=27 км/год
x2=(33-21)/2=6 км/год