с алгеброй Колебание струны задаётся уровнем h(t)=2sin , t =0 Найдите:а)амплитуду колебания;b)наименьший положительный период;c)область значений функции;d) постройте график функции на
Скорый поезд проходит 60 км в час а пассажирский 40 км. Найдите расстояние между городами, если скорый поезд преодолевает это расстояние на 2 часа быстрее, чем пассажирский.
ответ: 240 км
Объяснение:
Примем искомое расстояние равным S.
Тогда из формулы расстояние равно скорости, умноженной на время выразим время t=S:v . Скорый поезд проходит расстояние за S:60 часов, пассажирский за S:40 часов.
По условию S:40-S:40=2 часа. Приведя дроби к общему знаменателю, получим :
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство . Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить . Тогда получим, что , значит пересечение с осью x происходит в точке . Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.
Скорый поезд проходит 60 км в час а пассажирский 40 км. Найдите расстояние между городами, если скорый поезд преодолевает это расстояние на 2 часа быстрее, чем пассажирский.
ответ: 240 км
Объяснение:
Примем искомое расстояние равным S.
Тогда из формулы расстояние равно скорости, умноженной на время выразим время t=S:v . Скорый поезд проходит расстояние за S:60 часов, пассажирский за S:40 часов.
По условию S:40-S:40=2 часа. Приведя дроби к общему знаменателю, получим :
(3S-2S):120=2 =>
S=240 (км)
ответ: Расстояние между городами 240 км
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство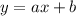 . Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить
. Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить 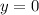 . Тогда получим, что
. Тогда получим, что 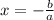 , значит пересечение с осью x происходит в точке
, значит пересечение с осью x происходит в точке 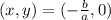 . Аналогично для оси ординат.
. Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.