1) x = ±
2) y =±
3) z = ±
4) k = ±
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
y^2 = 3
y = ±
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
z^2 = 3
z = ±
4) x^4 - 10x^2 + 9 = 0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
k^2 = 2
k = ±
6) 49y^4 - 48y^2 - 1 = 0
49t^2 - 48t - 1 = 0
t2 = -1 - посторонний
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
x1 = 1
x2 = 4
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
sinx=1,5 sinx=-1\2решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z -1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
![\sqrt[3]{2 + \sqrt{5} } + \sqrt[3]{2 - \sqrt{5} }](/tpl/images/4458/6112/c1faa.png)
1) x = ±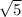
2) y =±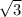
3) z = ±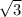
4) k = ±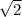
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±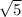
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
Обратная замена
y^2 = 3
y = ±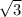
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =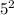
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
Обратная замена
z^2 = 3
z = ±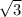
4) x^4 - 10x^2 + 9 = 0
Замена x^2 = t >0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
Обратная замена
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
Обратная замена
k^2 = 2
k = ±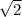
6) 49y^4 - 48y^2 - 1 = 0
Замена y^2 = t >0
49t^2 - 48t - 1 = 0
т.к. a + b + c = 0
t1 = 1
t2 = -1 - посторонний
Обратная замена
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
т.к. a + b + c = 0
x1 = 1
x2 = 4
Обратная замена
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
Замена x^2 = t >0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
Обратная замена
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
Замена sinx=t
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
Возвращаемся к замене
sinx=1,5 sinx=-1\2
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z