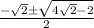1) Обозначим через:
х - число страниц, которое за 1 час печатает 1 машинистка
у - число страниц, которое за 1 час печатает 2 машинистка
2) Так как первая машинистка печатает на 1.5 часа быстрее,чем вторая, то первое уравнение будет:
а так как они вместе за 1 час печатают 30 страниц, то второе уравнение будет иметь вид:
х + у = 30
3) Из второго уравнения выразим у через х и подставим в первое уравнение:
у = 30 - х
Избавляемся от дроби, умножив все члены уравнения на х(30 - х), получаем:
30х - 900 + 30х = - 1,5х² + 45х
1,5х² + 15х -900 = 0
Разделим все члены уравнения на 1,5
х² + 10х -600 = 0
4) Решаем полученное квадратное уравнение:
D = 10² + 4*600 = 2500
√D = 50
x₁ = ( -10+50)/2 = 20
x₂ = (-10-50)/2 = - 30 отрицательное число, нам не подходит.
Значит первая машинистка печатает 20 страниц в час
5) Тогда 2 машинистка за 1 час печатает:
у = 30 - х = 30 - 20 = 10 страниц
6) Тогда вторая машинистка 60 страниц отпечатает за:
60/10 = 6 часов
ответ: За 6 часов
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
с замены
приводим к виду:
где:
добавим и вычтем из левой части уравнения 2 выражение , где s - некоторое число:
получим:
Пусть s - корень уравнения
Тогда уравнение 3 примет вид:
Избавляемся в уравнении 4 от знаменателя:
Раскроем скобки и получим:
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
Получим два квадратных уравнения:
Применяем этот метод для решения уравнения
Перепишем уравнение в полном виде:
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
ищем s:
подставляем p,q,r и s в квадратные уравнения 7 и 8:
Теперь находим x:
ответ:
1) Обозначим через:
х - число страниц, которое за 1 час печатает 1 машинистка
у - число страниц, которое за 1 час печатает 2 машинистка
2) Так как первая машинистка печатает на 1.5 часа быстрее,чем вторая, то первое уравнение будет:
а так как они вместе за 1 час печатают 30 страниц, то второе уравнение будет иметь вид:
х + у = 30
3) Из второго уравнения выразим у через х и подставим в первое уравнение:
у = 30 - х
30х - 900 + 30х = - 1,5х² + 45х
1,5х² + 15х -900 = 0
Разделим все члены уравнения на 1,5
х² + 10х -600 = 0
4) Решаем полученное квадратное уравнение:
D = 10² + 4*600 = 2500
√D = 50
x₁ = ( -10+50)/2 = 20
x₂ = (-10-50)/2 = - 30 отрицательное число, нам не подходит.
Значит первая машинистка печатает 20 страниц в час
5) Тогда 2 машинистка за 1 час печатает:
у = 30 - х = 30 - 20 = 10 страниц
6) Тогда вторая машинистка 60 страниц отпечатает за:
60/10 = 6 часов
ответ: За 6 часов
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
с замены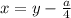
приводим к виду:
где:
добавим и вычтем из левой части уравнения 2 выражение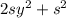 , где s - некоторое число:
, где s - некоторое число:
получим:
Пусть s - корень уравнения
Тогда уравнение 3 примет вид:
Избавляемся в уравнении 4 от знаменателя:
Раскроем скобки и получим:
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
Получим два квадратных уравнения:
Применяем этот метод для решения уравнения
Перепишем уравнение в полном виде:
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
ищем s:
подставляем p,q,r и s в квадратные уравнения 7 и 8:
Теперь находим x:
ответ: