Самостоятельная работа «Числовые неравенства. Свойства числовых неравенств»
2 вариант
1. Определить положительное или отрицательное число b, если:
а) -2.8b < 0 б) 85b > 0
2. Сравните числа a и b, если:
а) a – b >6 б) a – b < 0
в) a – b < -1 г) a – b = 0
3. Даны выражения 5c(c + 2) и 4c(c - 4).. Сравните их значения при c = - 3 ( >, < или =).
4. Известно, что a < b. Сравнить:
а) a – 2,1 и b – 2,1; б) 4 + a и 4 + b;
в) и ; г) и .
5. Доказать, что, если 6х + 5у < 3x + 8y, то x < y
6. Доказать, что, если (x - 2)² > x(x – 3) , то х < 4
(см. объяснение)
Объяснение:
Наименьшее значение, которое может принимать левая часть рано 8.
Наибольшее значение, которое может принимать правая часть равно 8.
Значит исходное равенство становится верным, если имеем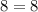
.
Тогда перейдем к системе уравнений:
Понятно, что вторая ее строчка решается несложно:
Поработаем теперь с первой:
Введем замену вида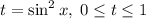
.
Тогда уравнение выше можно переписать:
Один из корней очевиден и равен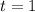
.
Понятно, что при
уравнение 
не имеет корней.
Выполним теперь обратную замену:
Тогда ответом будет:
Задание выполнено!
-4 < 9a + 5/6 < 3
-4 < 9а + 5/6;
9а + 5/6 < 3;
-4 - 9а - 5/6 < 0;
9а + 5/6 - 3 < 0;
-24 - 54а - 5 < 0;
54a + 5 - 18 < 0;
-54а - 29 < 0;
54а - 13 < 0;
-54а < 29;
54а < 13;
54а > -29;
54а < 13;
а > -29/54;
а < 13/54…
Если я, конечно, вычислила правильно, то Вам остаётся только провести координатную прямую, обозначить точки (это строгое неравенство, так что не ошибитесь), а дальше Вы знаете. К сожалению, я не уверена в правильности, очень странные числа, хоть и всё сто раз проверила. Но всё может быть)