Сд кесіндісінің ортасы 0 ( -4 ; 3 ) екені белгілі . С - 12 ; у ) . Дх , -2 ) болса , белгісіз координаталарды табыңдар . 2 ) ( ) А ( 3 ; 2 ) және В ( 6 ; -1 ) нүктелерінен ететін түзудің теңдеуін жазыныз 3 ) ( ) Шеңбердің тендеуі мына түрде берілген х ? + у — 6х + 4у + 4 = 0 Табындар : а ) шеңбердің центрінің координатасын ә ) шеңбердін радиусын 4 ) ( ) Егер А ( -2 ; 4 ) , B ( 3 ; 2 ) және С ( 5 , 6 ) нүктелері АВС үшбұрышынын тебелері болса , АК медианасынын ұзындығын табыңдар . 5 ) ) Төбелері А ( 0 ; 1 ) , В ( 4 : 3 ) co5 , 1 ) және Д. -1 ) нүктелері болатын тертөұрыштын тіктөртбұрыш болатынын дәләлденіз және оның ауданын табыңдар .
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).
Объяснение:
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).
Всего три пары -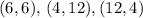
Объяснение:
Для того чтобы решить задачу, нужно правильно сформулировать проблему -
"Требуется найти все пары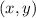
, где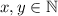 
так что 
."
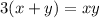Из равенства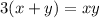
очевидно что 
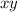делится на 3. Следовательно хотя бы одно из чисел 
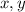делится на 3. Без огранчения общности, предположим что 
.
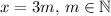Следовательно, высшеупомянотое равенство преообразовывается в
Заметим что отсюда выходит что,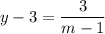
.
Т.к.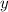
цело только и только тогда, когда 
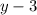цело, то следовательно, 3 должно делится на 
.
Число 3 делится только на четыре числа - 3, -3, 1, -1. Но лишь только два из них подходят - 3 и 1.
Следовательно,
Т.е.,
Отсюда получаем две пары -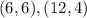
. Однако очевидно, что также и пара 
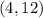подходит.