Смотри, ученика всего 23. У нас спрашивают, что сколько учеников имеет ТОЧНО более трёх конфет.
Нам сказано, что 7 из них имеют по 3 или менее конфет, а восемнадцать, по 2 или больше. А всего учеников-то 23!
2 или больше, может быть те восемнадцать имеют 3 конфеты, значит они входят в те 7. (ведь 7 учеников получили 3 или меньше, а 18 2 или больше, они могли получить 3 конфеты, ведь 2>3)
23-7=16 (конфет, которые ещё входят в список возможных детей, у которых больше 3-ёх конфет)
Но, ведь 18+7=25! А не 23, значит те, кто входят в число 18-ть (эти 2 человека из тех семи, кто имеет меньше двух конфет) Значит 2 человека ещё выпадают, у них по 3 или менее конфет. (Ведь нам не сказано, что 18 имеют по 3 или более, нам сказано, что 18 имеют 2 и более, значит могут иметь и 3 конфетки, и входить в число тех, кто получил меньше трёх, а не больше)
Значит 16-2=14 (ещё минус 2 человека)
Это число тех, кто точно имеет больше трёх конфет.
Для a = -0.5: x = 2 (как подстановка a в корень (2a + 3) )
Для a ∈ (-0.5, 1): x = 2a + 3
Для a ∈ [1; 3): x₁ = 2a + 3; x₂ = a - 1
Для a = 3: x = 2 (как подстановка a в корень (a - 1) )
Для a ∈ (3; +∞): x₁ = 2a + 3; x₂ = a - 1
Объяснение:
Можно заметить, что знаменатель уравнения представляет собой полный квадрат суммы. Ее можно свернуть в . Таким образом, мы сразу же можем сказать, что в итоге решения уравнения нужно исключить корни, равные 3а, так как в этом случае знаменатель обращается в нуль.
Чтобы дробь была равна нулю, необходимо, чтобы и числитель был равен нулю.
Найдем дискриминант этого уравнения
Дискриминант данного уравнения всегда неотрицательное число, поэтому как минимум одно решение будет всегда
Отсюда находим x:
Дополнительно определим, какие параметры a вполне допустимы:
Если a = 3, то корень единственный x = x₂ = a - 1 = 2
И если a = -0.5, то корень x = x₁ = 2a + 3 = 2
UPD:
Как верно заметили в комментариях, упустил одну деталь, и она связана с особенностями квадратного корня. Значение квадратного корня всегда неотрицательное число, поэтому справедливо неравенство:
Это значит, что корни, которые были получены через дискриминант, должны удовлетворять:
Это значит, что параметр a должен быть не меньше чем 2, чтобы существовало два корня
С другой стороны, если оно будет меньше 2, это еще не говорит о том, что и корней не будет. На отрезке [-1; 2) будет строго один корень, который равен 2a + 3. Других вариантов нет.
Смотри, ученика всего 23. У нас спрашивают, что сколько учеников имеет ТОЧНО более трёх конфет.
Нам сказано, что 7 из них имеют по 3 или менее конфет, а восемнадцать, по 2 или больше. А всего учеников-то 23!
2 или больше, может быть те восемнадцать имеют 3 конфеты, значит они входят в те 7. (ведь 7 учеников получили 3 или меньше, а 18 2 или больше, они могли получить 3 конфеты, ведь 2>3)
23-7=16 (конфет, которые ещё входят в список возможных детей, у которых больше 3-ёх конфет)
Но, ведь 18+7=25! А не 23, значит те, кто входят в число 18-ть (эти 2 человека из тех семи, кто имеет меньше двух конфет) Значит 2 человека ещё выпадают, у них по 3 или менее конфет. (Ведь нам не сказано, что 18 имеют по 3 или более, нам сказано, что 18 имеют 2 и более, значит могут иметь и 3 конфетки, и входить в число тех, кто получил меньше трёх, а не больше)
Значит 16-2=14 (ещё минус 2 человека)
Это число тех, кто точно имеет больше трёх конфет.
ответ: 14Для a ∈ (-∞; -1) корней не существует
Для a ∈ [-1; -0.5): x = 2a + 3
Для a = -0.5: x = 2 (как подстановка a в корень (2a + 3) )
Для a ∈ (-0.5, 1): x = 2a + 3
Для a ∈ [1; 3): x₁ = 2a + 3; x₂ = a - 1
Для a = 3: x = 2 (как подстановка a в корень (a - 1) )
Для a ∈ (3; +∞): x₁ = 2a + 3; x₂ = a - 1
Объяснение:
Можно заметить, что знаменатель уравнения представляет собой полный квадрат суммы. Ее можно свернуть в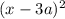
. Таким образом, мы сразу же можем сказать, что в итоге решения уравнения нужно исключить корни, равные 3а, так как в этом случае знаменатель обращается в нуль.
Чтобы дробь была равна нулю, необходимо, чтобы и числитель был равен нулю.
Найдем дискриминант этого уравнения
Дискриминант данного уравнения всегда неотрицательное число, поэтому как минимум одно решение будет всегда
Отсюда находим x:
Дополнительно определим, какие параметры a вполне допустимы:
Если a = 3, то корень единственный x = x₂ = a - 1 = 2
И если a = -0.5, то корень x = x₁ = 2a + 3 = 2
UPD:
Как верно заметили в комментариях, упустил одну деталь, и она связана с особенностями квадратного корня. Значение квадратного корня всегда неотрицательное число, поэтому справедливо неравенство:
Это значит, что корни, которые были получены через дискриминант, должны удовлетворять:
Это значит, что параметр a должен быть не меньше чем 2, чтобы существовало два корня
С другой стороны, если оно будет меньше 2, это еще не говорит о том, что и корней не будет. На отрезке [-1; 2) будет строго один корень, который равен 2a + 3. Других вариантов нет.