Sin^2x+sin^2 2x=0
673(1) выше тоже он написан

Используем свойства арифм. и геом. прогрессии:
х;у;z;...-члены прогрессии
х; у+8;z;... - арифметическая прогрессия
х;у+1;z+11 ...-геометр.прогрессия
{y^2=xz;                      y^2=xz;                       y^2=xz;                    y^2=x(2y-x+16)
{y+8=(x+z)/2;              2y+16=x+z;                  z=2y-x+16                z=2y-x+16
{(y+1)^2=x(z+11);        y^2+2y+1-xz-11x=0;      y^2+2y+1-y^2-11x=0; 2y-11x+1=0
 
Решаем {y^2=x(2y-x+16);      ((11x-1)^2)/4 -x(11x-1-x+16)=0
             {2y-11x+1=0;              y=(11x-1)/2
 
 121x^2-22x+1-4x(10x+15)=0
 121x^2-22x+1-40x^2-60x=0
81X^2- 82x+1=0
D1=41^2-81*1=1681-81=1600=40^2
x1=(41-40)/81=1/81;  x2=(41+40)/81=1
x=1; y=(11*1-1)/2=5; z=2*5-1+16=25
x=1/81;  y=1/81-1=-80/81; z=-160/81-1/81+16=1135/81-не является геом. прогрессией(может ошибка где? Проверьте
ответ. 1;5;25
;

x₁ = 2 + , y₁ = 2 - 3;

x₂ = 2 -, y₂ = - 3 - 2:

Объяснение:

{ху - х = 4

{2х - у = 7

Выразим y и подставим во второе уравнение

{xy - x = 4

{-y = 7 - 2x

Уберём минус перед y, помножив выражение на (-1)

{xy - x = 4

{y = 2x - 7

Подставляем полученное выражение вместо y

x * (2x - 7) - x = 4

2x² - 7x - x =4

2x² - 8x - 4 = 0

Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2

x² - 4x - 2 = 0

У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;

Но для начала проверим дискриминант

D = b² - 4ac

D = 16 - 4 * 1 * (-2)

D = 16 + 8 = 24

Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом

x₁,₂ =  

x₁ = = = 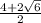2 +

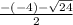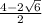x₂ = = = 2 -

Находим y, подставляя x

2 * (2 + ) - y₁ = 7

4 + 2 - y₁ = 7

- y₁ = 3 - 2

Убираем минус

y₁ = 2 - 3

Ищем y₂

2 * (2 - ) - y₂ = 7

4 - 2 - y₂ = 7

- y₂ = 3 + 2

Снова убираем минус

y₂ = - 3 - 2

ответ: x₁ = 2 + , y₁ = 2 - 3; x₂ = 2 -, y₂ = - 3 - 2;