ответ
sin x +cos x=корень(2) *корень(2)/2 (sin x+cos x)=
=корень(2) (корень(2)/2 *sin x+ корень(2)/2 *cos x)==корень (2)*(cos (pi/4)sin x+sin (pi/4)cos x)=
по формуле синуса суммы
корень(2) *sin (x+pi/4)<=
корень(2)*1=корень (2)
ответ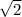
sin x +cos x=корень(2) *корень(2)/2 (sin x+cos x)=
=корень(2) (корень(2)/2 *sin x+ корень(2)/2 *cos x)=
=корень (2)*(cos (pi/4)sin x+sin (pi/4)cos x)=
по формуле синуса суммы
корень(2) *sin (x+pi/4)<=
корень(2)*1=корень (2)