Сколькими можно составить букет из 11 цветов если имеются 5 видов цветов

№1

а) √50 > 7

√50 > √7²

√50 > √49

б) 4√6 > 3√7

√4²*6 > √3²*7

√16*6 > √9*7

√96 > √63

№2

а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2

б) √(72*0,5)=√36=√6² = 6

в)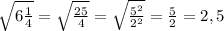

г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8

№3

а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6

б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11

в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3

№4

√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)

№5

№6

Система уравнгений:

{ x ^ 2 + y ^ 2 = 5;

x - y = 1;

{ x ^ 2 + y ^ 2 = 5;

x = 1 + y;

{ (1 + y) ^ 2 + y ^ 2 = 5;

x = 1 + y;

{ 1 + 2 * y + y ^ 2 + y ^ 2 = 5;

x = 1 + y;

{ 2 * y ^ 2 + 2 * y + 1 = 5;

x = 1 + y;

{ 2 * y ^ 2 + 2 * y + 1 - 5 = 0;

x = 1 + y;

{ 2 * y ^ 2 + 2 * y - 4 = 0;

x = 1 + y;

{ 2 * (y ^ 2 + y - 2) = 0;

x = 1 + y;

Найдем корни квадратного уравнения чеез дискриминант:

y ^ 2 + y - 2 = 0;

D = b ^ 2 - 4 * a * c = 1 - 4 * 1 * (- 2) = 9;

y1 = (- 1 + 3)/2 = 2/2 = 1;

y2 = (- 1 - 3)/2 = - 4/2 = - 2;

Тогда:

x1 = 1 + y1 = 1 + 1 = 2;

x2 = 1 + (- 2) = 1 - 2 = - 1;

ответ: (2; 1) и (- 1; - 2).

Объяснение: