б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
Смотри решение.
Объяснение:
решения (через дискриминант):
Порядок решения:
а. Записываем уравнение в исходном виде;
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
решения (через теорему Виетта):
Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.
Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.
Общая формула квадратного уравнения: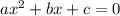
(для справок).
Теперь переходим к решению данного квадратного уравнения:
Арсений Стенура 3 года назад
Графиком линейной функции является ровная. Для её построения довольно 2-ух точек.
у=-4х+8
х=0; у=8 (0;8)
х=2; у=0 (2;0)
На координатной плоскости отмечаем эти точки и через них проводим прямую.
область определения:огромное количество всех реальных чмсел
точки скрещения с осью х:
-4х+8=0
-4х=-8
х=-8:(-4)
х=2
точки скрещения с осью у:
пусть х=0,тогда
у(0)=-4*0+8=8
область определения:огромное количество всех реальных чмсел
точки скрещения с осью х:
-4х+8=0
-4х=-8
х=-8:(-4)
х=2
точки скрещения с осью у:
пусть х=0,тогда
у(0)=-4*0+8=8
область определения:огромное количество всех реальных чмсел
точки скрещения с осью х:
-4х+8=0
-4х+8=0-4х=-8
-4х+8=0-4х=-8х=-8:(-4)
-4х+8=0-4х=-8х=-8:(-4)х=2
-4х+8=0-4х=-8х=-8:(-4)х=2 точки скрещения с осью у:
-4х+8=0-4х=-8х=-8:(-4)х=2 точки скрещения с осью у:пусть х=0,тогда
-4х+8=0-4х=-8х=-8:(-4)х=2 точки скрещения с осью у:пусть х=0,тогдау(0)=-4*0+8=8