Составить уравнение касательной к графику функции у= х2 – 3х +7, которая проходит через точку (0; -2), абсцисса точки касания положительна.

(см. объяснение)

Объяснение:

Пусть .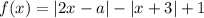

Тогда нужно, чтобы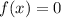 имело единственное решение.

Заметим, что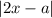 играет решающую роль в определении поведения функции (ее возрастания/убывания). Если он открывается со знаком +, то функция возрастает, иначе убывает.

Тогда промежуток убывания: .

Промежуток возрастания: .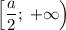

Единственное решение будет, если .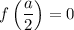

Получили уравнение:

Значит при данных значениях параметра a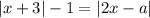 имеет единственное решение.

Бесконечное множество решений будет, если левая и правая части совпадают (то есть графики наложатся). Но это невозможно, так как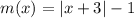 более широкий (прямой угол), чем 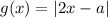(острый угол) и величина угла от параметра никак не зависит.

Задание выполнено!

Комментарий:

Можно было решать задачу, строя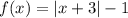 и 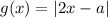. Первый график имеет фиксированное положение, а второй бегает влево-вправо. Тогда тоже легко сделать требуемый вывод.

-62

Объяснение:

f(x)=ax²+bx+c

Определим коэффициенты a, b, с.

1) Коэффициент а находим по формуле y=a(x-m)²+n, где (m;n) - координаты вершины параболы, а (х;у) - координата любой точки параболы, например, (1;1).

m=2; n=2

a(1-2)²+2=1

a(-1)²=-1

a*1=-1

a=-1

2) Коэффициент b находим из формулы для вершины параболы:

  -b/2a = m

  b = -m*2a =-2*2*(-1)=4

3) Коэффициент с найдём как ординату пересечения параболы с осью Оу. Искомая точка (0;-2), значит, с=-2

4) Запишем уравнение параболы: f(x) = -x²+4x-2

5) Находим f(10):

f(10)= -10²+4*10-2 = -100+40-2 = -62