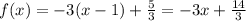Общий вид уравнения касательной:
Вычислим значение функции в точке х0=1, т.е.
Найдем теперь производную функции и затем найти ее значение в т. х0=1
Уравнение касательной
Общий вид уравнения касательной: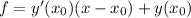
Вычислим значение функции в точке х0=1, т.е.
Найдем теперь производную функции и затем найти ее значение в т. х0=1
Уравнение касательной