Спортивный клуб арендует тренажерный зал и зал для занятий акробатикой. Тренажерный зал имеет форму
прямоугольника, длина которого на 6 м больше его ширины.
Длина зала для занятий акробатикой на 9 м, а ширина
на 12 м больше длины и ширины тренажерного зала соответственно, а его площадь в три раза больше площади тренажерного зала. Найдите размеры и площадь тренажерного зала
Ширина примерно равна 11м 53см, тогда длинна 17м 53см.
Площадь: 202кв. м
Объяснение:
Если мы возьмём ширину тренажёрного зала за "a", то длинна будет равна a+6.
Тогда ширина акробатического зала будет равна а+9, а ширина a+18(6+12).
Зная, что площадь акробатического зала равна 3 площади тренажёрного, то составляем уравнение:
3(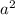
+6a)=(a+9)(a+18) - формула площади: S=x*y(где x - длинна, y - ширина)
Раскрываем скобки:
3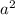
+18a=
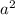+9a+18a+162
Переносим в одну часть:
2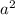
-9а-162=0
Получили квадратичное уравнение, решаем методом дискриминанта:
D=b-4ac=81+1296=1377
D>0 => 2 корня уравнения.
x1,2=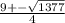
x1=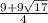
x2=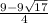
x1=-7.03 x2=11.53
Так как длинна не может быть отрицательна, ответ x2=a=11.53м
Подставляем а и найдём неизвестные величины.
Пусть x - это ширина тренажерного зала. Тогда его длина будет x + 6, так как длина на 6 м больше ширины.
Также у нас есть информация о зале для занятий акробатикой. Его длина равна 9 м, а его ширина равна x + 12 (длине тренажерного зала) и x + 12 (ширине тренажерного зала) соответственно.
Теперь у нас есть все необходимые данные для нахождения площадей обоих залов и решения задачи.
Площадь тренажерного зала равна произведению его длины на ширину:
Площадь тренажерного зала = (x + 6) * x
Площадь зала для занятий акробатикой равна произведению его длины на ширину, умноженную на 3:
Площадь зала для занятий акробатикой = 9 * (x + 12) * (x + 12) * 3
Согласно условию задачи, площадь зала для занятий акробатикой в три раза больше площади тренажерного зала, поэтому мы можем установить равенство:
9 * (x + 12) * (x + 12) * 3 = (x + 6) * x
Теперь нам нужно решить это уравнение для определения значения x и далее найти длину и ширину тренажерного зала.
Для упрощения уравнения мы можем сократить общие множители:
27 * (x + 12) * (x + 12) = x * (x + 6)
Раскроем скобки и упростим уравнение:
27 * (x^2 + 24x + 144) = x^2 + 6x
Умножим все члены уравнения на 27 и распространим умножение:
27x^2 + 648x + 3888 = x^2 + 6x
Теперь соберем все члены с переменной x в одну сторону, а все числовые члены в другую сторону:
27x^2 - x^2 + 648x - 6x - 3888 = 0
Упростим эту часть уравнения:
26x^2 + 642x - 3888 = 0
Теперь у нас есть квадратное уравнение, которое мы можем решить с помощью формулы дискриминанта:
x = (-b ± √(b^2 - 4ac)) / 2a
Где a = 26, b = 642, c = -3888.
По формуле дискриминанта:
D = b^2 - 4ac
D = 642^2 - 4 * 26 * -3888
D = 412164 - (-404736)
D = 412164 + 404736
D = 816900
Теперь мы можем использовать формулу для нахождения значения x:
x = (-642 ± √816900) / (2 * 26)
x = (-642 ± √816900) / 52
x = (-642 ± 904) / 52
Теперь у нас есть два значения для x:
x1 = (-642 + 904) / 52
x2 = (-642 - 904) / 52
Вычислим каждое значение:
x1 = 262 / 52
x1 = 5
x2 = -1546 / 52
x2 = -29.615
Мы исключаем отрицательное значение x, поскольку размер не может быть отрицательным. Это значит, что ширина тренажерного зала равна 5 м.
Теперь, используя это значение, мы можем найти длину тренажерного зала:
Длина тренажерного зала = x + 6 = 5 + 6 = 11 м
Таким образом, размеры тренажерного зала составляют 5 м (ширина) и 11 м (длина).
Осталось найти площадь тренажерного зала путем умножения его длины на ширину:
Площадь тренажерного зала = 5 * 11 = 55 м^2