Среди действительных чисел выбери иррациональное число
корень из 16
1/корень из 25
0,2
3/10
1/корень 7

между какими натуральными числами находится число
корень 27 -1
корень 25-1

вычисли рациональным корень 44100=корень 441 *корень 100

Показать ответ

Ответ:

lexazykov20014

21.04.2021 23:22

А6 - 1,3

В1 - (20;20)

В2 - (2;0)

С1 - 2

С2 - (фотка)

Объяснение:

А6. решение на фото

В1. чтобы найти координату пересечения графиков функции нужно их прировнять

$4x=2x+10\\4x-2x=10\\2x=10\\x=5$

Найдём Y если подставим полученное значение Х в функцию (можно подставить в любую)

$y=4x\\y=4*5\\ y=20$

$y=2x+10\\y=2*5+10\\y=20$

Точка пересечения графиков функции имеет следующие координаты (20;20)

В.2

Ось абсцисс - это ось ОХ

Чтобы найти координату пересечение графика функции с осью абсцисс

Нужно прировнять Y к 0, так как нам нужно пересечение графика функции с осью абсцисс

$y=x-2\\0=x-2\\x=2$

Точка пересечение графика функции с осью абсцисс имеет следующие координаты (2;0)

С.1

Мы имеем функцию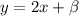 $y=2x+\beta$ и точку с координатами (0;2)

Чтобы найти b мы подставим координаты точки в функцию

$y=2x+\beta \\2=2*0+\beta \\2=\beta$

С.2 решение на фото

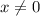( $x\neq 0$ так как при делении любого выражения на 0 получается неопределённое выражение)

ответьте хотя бы на один из вопросов ( но лучше на все))

0,0(0 оценок)

Ответ:

lera933737

10.11.2022 00:46

Б) f(x)=4-2x
f`(x)=(4-2x)`=(4)`-(2x)`=0-2·(x)`=-2·1=-2
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (-2)
f`(0,5)=f`(-3)=-2

в) f(x)=3x-2
f`(x)=(3x-2)`=(3х)`-(2)`=3·(x)`-0=3·1=3
Применили правила:
производная суммы( разности) равна сумме( разности) производных
Производная постоянной (C)`=0
Постоянный множитель можно вынести за знак производной
(х)`=1
Производная принимает во всех точках одно и то же значение (3)
f`(5)=f`(-2)=3

0,0(0 оценок)

Популярные вопросы: Алгебра