Стрелок производит 4 выстрела. вероятность попадания в мишень при каждом выстреле равна 0,45. за каждое попадание стрелку засчитывается 5 очков. построить ряд распределения числа выбитых очков. описать полностью действия с формулой.

Пусть случайная величина X - число выбитых очков; также добавим что эта случайная величина распределена по биномиальному закону.

1) Стрелок выбил 0 очков, т.е. он не попал ни разу в мишень. Такова вероятность будет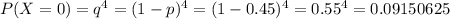

2) Стрелок выбил 5 очков, т.е. в мишень он попал один раз. Вероятность того, что при 4 выстрелах стрелок попадет только один раз, равна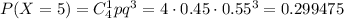

3) Стрелок выбил 10 очков, т.е. в мишень он попадает два раза. Вероятность того, что при четырех выстрелах стрелок попадет ровно два раза равна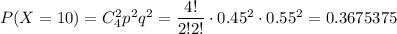

4) Стрелок выбил 15 очков, т.е. в мишень стрелок попал три раза. Вероятность того, что при 4 выстрелах стрелок попал ровно 3 раза равна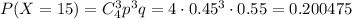

5) Стрелок выбил 20 очков, т.е. он в мишень попал ровно 4 раза. Такова вероятность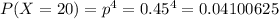

Закон распределения случайной величины X:

Xi           0                  5                10                15                  20

Pi  0.09150625  0.299475  0.3675375  0.200475   0.04100625