1. пусть эти два числа будут a и b, тогда запишем систему
выявим а
подставляем a в первое выражение и получается
9 - b - b = 17
9 - 2b = 17
-2b = 17-9
-2b = 8
b = -4
и теперь значение b подставляем во второе выражение, чтобы найти a
a = 9 - (-4)
a = 9 + 4
a = 13
ответ: числа 13 и -4
2. пусть эти два числа будут a и b, тогда запишем систему
выявим a в первом выражении
a = 23-b
и теперь подставим это значение во второе выражение
(23-b)b = 102
23b-b^2 = 102
-b^2 + 23b -102 =0 --решаем квадратное уравнение через дискриминант
D = 529 -408= 121
1b = = 17 a=23-17=6
2b = = 6 a=23-6=17
ответ: числа 17 и 6
3. пусть эти два числа будут a и b, тогда запишем систему
a = 12+b
(12+b)b=364
b^2 + 12b =364
b^2 +12b - 364 = 0 --решаем квадратное уравнение через дискриминант
D= 144 + 1456= 1600
1b = = -26 a=12-26=-14
2b = = 14 a=12+14=26
ответ: числа -26 и -14; 14 и 26
В решении.
Объяснение:
Розв'яжіть квадратну нерівність
1) 2х²+10х+8>0
Приравнять к нулю и решить квадратное уравнение:
2х² + 10х + 8 = 0
D=b²-4ac = 100 - 64 = 36 √D=6
х₁=(-b-√D)/2a
х₁=(-10-6)/4
х₁= -16/4
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-10+6)/4
х₂= -4/4
х₂= -1;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = -4 и х = -1.
у > 0 (как в неравенстве) при х от -∞ до х= -4 и от х= -1 до +∞ (парабола выше оси Ох).
Решения неравенства: х∈(-∞; -4)∪(-1; +∞).
Неравенство строгое, скобки круглые.
2) 3х²+11х—4≤0
3х² + 11х - 4 = 0
D=b²-4ac = 121 + 48 = 169 √D=13
х₁=(-11-13)/6
х₁= -24/6
х₂=(-11+13)/6
х₂=2/6
х₂=1/3;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = -4 и х = 1/3.
у <= 0 (как в неравенстве) при х от х= -4 до х= 1/3 (парабола ниже оси Ох).
Решения неравенства: х∈[-4; 1/3].
Неравенство нестрогое, скобки квадратные.
3) -5х²-3х+2>0
-5х² - 3х + 2 = 0/-1
5х² + 3х - 2 = 0
D=b²-4ac = 9 + 40 = 49 √D=7
х₁=(-3-7)/10
х₁= -10/10
х₁= -1;
х₂=(-3+7)/10
х₂=4/10
х₂=0,4;
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х = -1 и х = 0,4.
у > 0 (как в неравенстве) при х от х= -1 до х= 0,4 (парабола выше оси Ох).
Решения неравенства: х∈(-1; 0,4).
1. пусть эти два числа будут a и b, тогда запишем систему
выявим а
подставляем a в первое выражение и получается
9 - b - b = 17
9 - 2b = 17
-2b = 17-9
-2b = 8
b = -4
и теперь значение b подставляем во второе выражение, чтобы найти a
a = 9 - (-4)
a = 9 + 4
a = 13
ответ: числа 13 и -4
2. пусть эти два числа будут a и b, тогда запишем систему
выявим a в первом выражении
a = 23-b
и теперь подставим это значение во второе выражение
(23-b)b = 102
23b-b^2 = 102
-b^2 + 23b -102 =0 --решаем квадратное уравнение через дискриминант
D = 529 -408= 121
1b =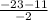 = 17 a=23-17=6
= 17 a=23-17=6
2b =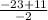 = 6 a=23-6=17
= 6 a=23-6=17
ответ: числа 17 и 6
3. пусть эти два числа будут a и b, тогда запишем систему
выявим a в первом выражении
a = 12+b
и теперь подставим это значение во второе выражение
(12+b)b=364
b^2 + 12b =364
b^2 +12b - 364 = 0 --решаем квадратное уравнение через дискриминант
D= 144 + 1456= 1600
1b =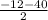 = -26 a=12-26=-14
= -26 a=12-26=-14
2b =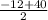 = 14 a=12+14=26
= 14 a=12+14=26
ответ: числа -26 и -14; 14 и 26
В решении.
Объяснение:
Розв'яжіть квадратну нерівність
1) 2х²+10х+8>0
Приравнять к нулю и решить квадратное уравнение:
2х² + 10х + 8 = 0
D=b²-4ac = 100 - 64 = 36 √D=6
х₁=(-b-√D)/2a
х₁=(-10-6)/4
х₁= -16/4
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-10+6)/4
х₂= -4/4
х₂= -1;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = -4 и х = -1.
у > 0 (как в неравенстве) при х от -∞ до х= -4 и от х= -1 до +∞ (парабола выше оси Ох).
Решения неравенства: х∈(-∞; -4)∪(-1; +∞).
Неравенство строгое, скобки круглые.
2) 3х²+11х—4≤0
Приравнять к нулю и решить квадратное уравнение:
3х² + 11х - 4 = 0
D=b²-4ac = 121 + 48 = 169 √D=13
х₁=(-b-√D)/2a
х₁=(-11-13)/6
х₁= -24/6
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-11+13)/6
х₂=2/6
х₂=1/3;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х = -4 и х = 1/3.
у <= 0 (как в неравенстве) при х от х= -4 до х= 1/3 (парабола ниже оси Ох).
Решения неравенства: х∈[-4; 1/3].
Неравенство нестрогое, скобки квадратные.
3) -5х²-3х+2>0
Приравнять к нулю и решить квадратное уравнение:
-5х² - 3х + 2 = 0/-1
5х² + 3х - 2 = 0
D=b²-4ac = 9 + 40 = 49 √D=7
х₁=(-b-√D)/2a
х₁=(-3-7)/10
х₁= -10/10
х₁= -1;
х₂=(-b+√D)/2a
х₂=(-3+7)/10
х₂=4/10
х₂=0,4;
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х = -1 и х = 0,4.
у > 0 (как в неравенстве) при х от х= -1 до х= 0,4 (парабола выше оси Ох).
Решения неравенства: х∈(-1; 0,4).
Неравенство строгое, скобки круглые.