1.) Из квадратного арифметического корня нельзя вычислить отрицательное число
2.) Тоже самое как и первое, при сложении квадратных корней нужно потребовать чтобы правая часть было больше или равна нулю
3.) Даже если бы был бы меньше нуля или равен нулю, подкорневое выражение было бы меньше нуля.
4.) Если возвести обе части в квадрат и попробовать решить уравнение дискрименантом, корней не будет т.к. D < 0.
5.) Тоже самое как и с предыдущим, возведя обе части в квадрат, мы получим - нет корней.
6.) Аналогично с предыдущим, решаем квадратное уравнение, D < 0.
Объяснение:
(х-5)(х+3) меньше 0 4х²-9 больше 0 2х²+7-4≤0
х-5 меньше 0 2х-3 больше 0 2х²+7-4=0
х+3 меньше 0 2х больше 3 D=b²-4ac=49-4*2*-4=81
х1 меньше 5 х больше 1,5 x1,2=-b±√D/2a
х2 меньше -3 х∈(1,5;∞) x1=-7+9/4=0.5
x∈(-3;5) x2=-7-9/4=-2.75
x∈[-2.75;0.5]
1.) Из квадратного арифметического корня нельзя вычислить отрицательное число
2.) Тоже самое как и первое, при сложении квадратных корней нужно потребовать чтобы правая часть было больше или равна нулю
3.) Даже если бы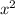
был бы меньше нуля или равен нулю, подкорневое выражение было бы меньше нуля.
4.) Если возвести обе части в квадрат и попробовать решить уравнение дискрименантом, корней не будет т.к. D < 0.
5.) Тоже самое как и с предыдущим, возведя обе части в квадрат, мы получим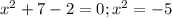
- нет корней.
6.) Аналогично с предыдущим, решаем квадратное уравнение, D < 0.
Объяснение:
(х-5)(х+3) меньше 0 4х²-9 больше 0 2х²+7-4≤0
х-5 меньше 0 2х-3 больше 0 2х²+7-4=0
х+3 меньше 0 2х больше 3 D=b²-4ac=49-4*2*-4=81
х1 меньше 5 х больше 1,5 x1,2=-b±√D/2a
х2 меньше -3 х∈(1,5;∞) x1=-7+9/4=0.5
x∈(-3;5) x2=-7-9/4=-2.75
x∈[-2.75;0.5]
Объяснение: