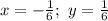Одна сторона буде х см, а інша (х + 23) см. Ці сторони разом з діагоналлю (37 см) утворюють прямокутний трикутник. Скориставшись т. Піфагора, складаємо рівняння: х² + (х + 23)² = 37².
х² + х² + 23² + 46х = 37²;
2х² + 46х + 23² - 37² = 0;
2х² + 46х + (23 - 37)(23 + 37) = 0;
2х² + 46х - 14·60 = 0;
х² + 23х - 14·30 = 0;
x₁ = 35; x₂ = 12.
Отже, одна сторона буде 35 см, або 12 см, тоді друга сторона буде 35 - 23 = 12 см або 35 - 12 = 23 см. Тобто маємо прямокутник із сусідніми сторонами 35 см і 12 см, периметр якого дорівнює 2(35 + 12) = 94 см.
Смысл задачи: найти такие x и y, чтобы это равенство было справедливо при всех допустимых значений a (то есть для всех, кроме -4 и 2).
1-й
2-й
Запишем равенство в виде
знаменатели в левой и правой части совпадают, поэтому совпадают числители:
x(a-2)+y(a+4)=1.
Дальше у нас есть две возможности рассуждения. При первой подставляем в это равенство a=2, находя при этом y=1/6, а затем подставляем a=-4, находя x=-1/6.
При втором рассуждения запишем равенство в виде
(x+y)a+(-2x+4y)=1. Поскольку это равенство должно быть справедливо при всех значениях a, получаем систему решив которую, получим те же значения x и y.
Одна сторона буде х см, а інша (х + 23) см. Ці сторони разом з діагоналлю (37 см) утворюють прямокутний трикутник. Скориставшись т. Піфагора, складаємо рівняння: х² + (х + 23)² = 37².
х² + х² + 23² + 46х = 37²;
2х² + 46х + 23² - 37² = 0;
2х² + 46х + (23 - 37)(23 + 37) = 0;
2х² + 46х - 14·60 = 0;
х² + 23х - 14·30 = 0;
x₁ = 35; x₂ = 12.
Отже, одна сторона буде 35 см, або 12 см, тоді друга сторона буде 35 - 23 = 12 см або 35 - 12 = 23 см. Тобто маємо прямокутник із сусідніми сторонами 35 см і 12 см, периметр якого дорівнює 2(35 + 12) = 94 см.
Відповідь: 94 см.
Смысл задачи: найти такие x и y, чтобы это равенство было справедливо при всех допустимых значений a (то есть для всех, кроме -4 и 2).
1-й
2-й
Запишем равенство в виде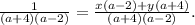
знаменатели в левой и правой части совпадают, поэтому совпадают числители:
x(a-2)+y(a+4)=1.
Дальше у нас есть две возможности рассуждения. При первой подставляем в это равенство a=2, находя при этом y=1/6, а затем подставляем a=-4, находя x=-1/6.
При втором рассуждения запишем равенство в виде
(x+y)a+(-2x+4y)=1. Поскольку это равенство должно быть справедливо при всех значениях a, получаем систему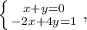
решив которую, получим те же значения x и y.
ответ: