ОДЗ:
Разложим первую скобку в знаменателе на множители. Для этого решим уравнение
Подставим это разложение в исходное выражение и выполним преобразование:
Очевидно, что:
1) выражение будет всегда положительным при любых x ≠ -2, то есть не влияет на условия неравенства;
2) выражение будет неотрицательным при любых x.
Решение исходного неравенства сводится к решению неравенства
с учётом "выколотой" точки x = -2
Имеем две точки: x = -1 и x = 5. Определим знаки последнего выражения на получившихся интервалах:
ответ:
ОДЗ:
Разложим первую скобку в знаменателе на множители. Для этого решим уравнение
Подставим это разложение в исходное выражение и выполним преобразование:
Очевидно, что:
1) выражение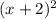
будет всегда положительным при любых x ≠ -2, то есть не влияет на условия неравенства;
2) выражение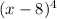
будет неотрицательным при любых x.
Решение исходного неравенства сводится к решению неравенства
с учётом "выколотой" точки x = -2
Имеем две точки: x = -1 и x = 5. Определим знаки последнего выражения на получившихся интервалах:
ответ:![(-\infty;\;-2)\cup(-2;\;-1]\cup(5;\;+\infty)](/tpl/images/1165/8321/f59e9.png)