Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х -2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Составьте какое-нибудь уравнение с двумя переменными,график которого проходит через точку A(3;-3)
" решение " : какое-нибудь уравнение например
x*y = - 9 (гипербола) или у = x² - 4x (парабола)
|| 3*(-3)= - 9 или - 3 = 3² - 4*3 ||
* * * * * * * * * * * * * * * * * * * * * * *
Для определенности меняем условия задачи
Составьте какое-нибудь ЛИНЕЙНОЕ уравнение с двумя переменными , график которого проходит через точку A(3;-3) .
Решение : Общий вид таких уравнений : a*x +b*y + c =0 , где a , b , с постоянные и a² +b² ≠ 0
Если график проходит через точку A(3 ; - 3) , значит
a*3 +b*(-3) + c =0 ⇒ c = 3b - 3a и получаем вид уравнения
a*x +b*y + 3b -3a = 0 || ≡ ax +by + 3b -3a = 0 ||
Вместо a и b можно поставить любое значение одновременно не равные нулю
например :
1) a = 2 , b = 5 ⇒ 2x +5y +9 =0
или
2) a = 1 , b = - 1 ⇒ x - y - 6 = 0 || x -y =6 ; y = x - 6 ||
1)Решение системы неравенств [-2, (-1+√73)/4]
2)Решение системы неравенств х∈(0,2, 1)
Объяснение:
1. Решите систему неравенств:
3х+4≤4х+6
х-5≤4-2х²
Во втором неравенстве перенесём все члены уравнения в левую часть, приравняем к нулю и решим, как квадратное уравнение:
х-5-4+2х²≤0
2х²+х-9=0
х₁,₂=(-1±√1+72)/4
х₁,₂=(-1±√73)/4
х₁=(-1-√73)/4 ≈ -9,5
х₂=(-1+√73)/4 ≈ 7,5
Начертим СХЕМУ параболы, которую обозначает данное уравнение (ничего вычислять не надо). Просто начертим схематично оси, параболу с ветвями вверх, и отметим на оси Ох точки х₁ ≈ -9,5 и
х₂ ≈ 7,5. Ясно видно, что у<0 при х от -9,5 до 7,5, то есть,
решение второго неравенства х∈[(-1-√73)/4, (-1+√73)/4]
Решим первое неравенство.
3х+4≤4х+6
3х-4х ≤6-4
-х ≤2
х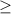
-2 знак меняется
Решение первого неравенства х∈[-2, ∞).
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств [-2, (-1+√73)/4] х от -2 до 7,5.
Неравенства нестрогие, скобки квадратные.
2. Решите двойное неравенство -3<2-5х<1
Решается как система:
2-5х>-3
2-5х<1
-5х> -3-2
-5x<1-2
-5x> -5
-5x< -1
x<1 знак меняется x ∈(-∞, 1) решение 1-го неравенства
x>0,2 знак меняется x ∈(0,2, ∞) решение 2-го неравенства
Отметим на числовой оси решение первого неравенства и решение второго, чтобы найти пересечение решений, то есть, такое решение, которое подходит и первому, и второму неравенству.
Решение системы неравенств х∈(0,2, 1)
Неравенства строгие, скобки круглые.