ответ: k=6 .
Числа, на которые делится число 24, - это k=1, 2, 3, 4, 6, 8 , 12 , 24 .
Из них нам подходят числа 2 , 3, 4, 6, так как тогда выражения (k-2) и
(7-k) будут положительны .
Тогда показатели степеней при k=2 будут 24/2=12 , 2-2=0 , 7-2=5 , старший показатель степени = 12 .
При k=3 показатели степеней равны 24/3=8 , 3-2=1 , 7-3=4 , старший показатель степени = 8 .
При k=4 показатели степеней равны 24/4=6 , 4-2=2 , 7-4=3 , старший показатель степени = 6 .
При k=6 показатели степеней равны 24/6=4 , 6-2=4 , 7-6=1 , старший показатель степени = 4 .
Наименьшую степень многочлен имеет при k=6 .
ответ:
Объяснение:
Решить совокупность неравенств:
Решим каждое неравенство отдельно, а в ответ запишем все решения данных неравенств.
1. Решим первое неравенство.
Раскроем скобки. Перенесем неизвестные влево, известные вправо. Не забываем при переносе через знак неравенства поменять знаки на противоположные.
Приведем подобные члены:
2. Аналогично решим второе неравенство.
Отметим решения на числовой оси и объединим промежутки.
См. рис.
Получили ответ:
#SPJ1
ответ: k=6 .
Числа, на которые делится число 24, - это k=1, 2, 3, 4, 6, 8 , 12 , 24 .
Из них нам подходят числа 2 , 3, 4, 6, так как тогда выражения (k-2) и
(7-k) будут положительны .
Тогда показатели степеней при k=2 будут 24/2=12 , 2-2=0 , 7-2=5 , старший показатель степени = 12 .
При k=3 показатели степеней равны 24/3=8 , 3-2=1 , 7-3=4 , старший показатель степени = 8 .
При k=4 показатели степеней равны 24/4=6 , 4-2=2 , 7-4=3 , старший показатель степени = 6 .
При k=6 показатели степеней равны 24/6=4 , 6-2=4 , 7-6=1 , старший показатель степени = 4 .
Наименьшую степень многочлен имеет при k=6 .
ответ: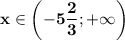
Объяснение:
Решить совокупность неравенств:
Решим каждое неравенство отдельно, а в ответ запишем все решения данных неравенств.
1. Решим первое неравенство.
Раскроем скобки. Перенесем неизвестные влево, известные вправо. Не забываем при переносе через знак неравенства поменять знаки на противоположные.
Приведем подобные члены:
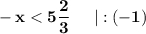
Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.2. Аналогично решим второе неравенство.
Отметим решения на числовой оси и объединим промежутки.
См. рис.
Получили ответ: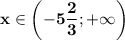
#SPJ1