Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ. а) 2x^2 + 8х + 20 ≥ 0; Б) —x^2— 10x + 25 > 0; c)х^2 + 3x +2 ≤ 0 d) — 4х^2 – 4 >0. 1) Неравенство не имеет решений. 2) Решением неравенства является вся числовая прямая, 3) Решением неравенства является одна точка. 4) Решением неравенства является закрытый промежуток. 5) Решением неравенства является открытый промежуток. 6) Решением неравенства является объединение двух промежутков.
Пусть х-скорость первого пешехода,тогда х-1 - скорость второго пешехода. ТАк как путь и того и другого равен 5 км/ч,тогда скорость первого пешехода 5/x, а второго 5/x-1. Ещ нам известно,что второму понадобилось на 15 минут больше чем первому. ПОэтому составим уравнение:
5/x-1 - 5/x=15
x(x-1)
домножим каждую дробь на недостающий множитель,получим:
5х-5х+5-15х^2-15х=-15х^2-15х+5---это числитель
х^2-хзнаменатель,он должен быть не равен 0(так как знаменатель отличен от нуля)значит х не равен 0 и не равен 1
Это уравнение окружности с центром (1;0) и радиусом R = 1.
Пусть общий вид неизвестной прямой y = kx + b. Эта прямая параллельна прямой x + 2y = 0, т.е. у параллельных прямых угловые коэффициенты равны: k = -0.5. Получаем y = -0.5x + b. Известно, что прямая y = -0.5x + b проходит через центр окружности (1;0), т.е., подставляя координаты точки центра окружности, мы найдем коэффициент b
Таким образом, нашли неизвестную прямую y = -0.5x + 0.5 или x + 2y - 1 = 0
Наглядно нарисуем графики и данный треугольник.
Найдем уравнение прямой, проходящей через точку O(0;0) и перпендикулярно прямой x + 2y - 1 = 0.
Прямая, проходящая через точку M(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнением:
Далее найдем координаты точки пересечения двух прямых y = -0.5x + 0.5 и y = 2x.
Точка D имеет координаты . Расстояние от точки О до точки D:
∠AOB опирается на диаметр AB, следовательно, ∠AOB = 90°, а диаметр окружности в два раза больше радиуса, т.е. AB = 2R = 2 * 1 = 2.
Пусть х-скорость первого пешехода,тогда х-1 - скорость второго пешехода. ТАк как путь и того и другого равен 5 км/ч,тогда скорость первого пешехода 5/x, а второго 5/x-1. Ещ нам известно,что второму понадобилось на 15 минут больше чем первому. ПОэтому составим уравнение:
5/x-1 - 5/x=15
x(x-1)
домножим каждую дробь на недостающий множитель,получим:
5х-5х+5-15х^2-15х=-15х^2-15х+5---это числитель
х^2-хзнаменатель,он должен быть не равен 0(так как знаменатель отличен от нуля)значит х не равен 0 и не равен 1
а числитель равен о
-15х^2 -15х +5=0 разделим обе части на - 5
3х^2+3х-1=0
находим дискриминант 9+12=21
Это уравнение окружности с центром (1;0) и радиусом R = 1.
Пусть общий вид неизвестной прямой y = kx + b. Эта прямая параллельна прямой x + 2y = 0, т.е. у параллельных прямых угловые коэффициенты равны: k = -0.5. Получаем y = -0.5x + b. Известно, что прямая y = -0.5x + b проходит через центр окружности (1;0), т.е., подставляя координаты точки центра окружности, мы найдем коэффициент b
Таким образом, нашли неизвестную прямую y = -0.5x + 0.5 или x + 2y - 1 = 0
Наглядно нарисуем графики и данный треугольник.
Найдем уравнение прямой, проходящей через точку O(0;0) и перпендикулярно прямой x + 2y - 1 = 0.
Прямая, проходящая через точку M(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнением:
Далее найдем координаты точки пересечения двух прямых y = -0.5x + 0.5 и y = 2x.
Точка D имеет координаты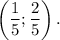
. Расстояние от точки О до точки D:
∠AOB опирается на диаметр AB, следовательно, ∠AOB = 90°, а диаметр окружности в два раза больше радиуса, т.е. AB = 2R = 2 * 1 = 2.
Площадь треугольника AOB:
ответ: 1/√5 кв. ед..