Укажите значение а, при которых данная функция убывает на r и имеет критическую точку, а также те значения а при которых функция убывает на r и не имеет критических точек
Вообще, исходя из определений, критическая точка для функции одного переменного - это точка, в которой производная функции равна 0.
Далее, для пункта 1 нам нужно, чтобы исходная функция убывала на (-∞;+∞), для этого производная должна быть неположительной на этом же интервале и в одной точке должна быть равной нулю.
График производной - парабола (за исключением одного случая), причем её направление зависит от выражения с параметром. Нам нужно, чтобы парабола в одной точке касалась оси ОХ, а вся остальная парабола находилась ниже оси ОХ. То есть, её ветви должны быть направлены вниз.
Но для начала рассмотрим тот случай, когда a=-1 и это не парабола.
. Видно, что исходная функция будет и возрастать, и убывать, так что a=-1 не подходит нам.
Вернемся к параболе. Направление ветвей вниз - ограничение
Условие, когда один корень - D=0 в уравнении y'=0
Тогда имеем два значения a:
Учитывая ограничение a<-1 (корень из 6 больше 2), берем только a2.
Теперь к пункту 2, когда критических точек нет. На самом деле, всю работу мы почти сделали. Ещё раз выпишем производную
Теперь нам надо, чтобы даже касаний оси ОХ этой параболой не было. Тогда получается необходимость отсутствия корней уравнения y'=0. Этот случай при D<0 (корней нет, а сама парабола находится ниже оси ОХ, главное будет потом учесть ограничение на направление ветвей вниз - a<-1)
Чтобы решить это неравенство, нужно исследовать D как функцию, найти её нули и методом интервалов решить неравенство. Но нули её мы как раз нашли. Это
Методом интервалов получим левый крайний и правый крайний промежуток a∈∪
Но теперь надо учесть ограничение a<-1. Тогда правый промежуток нам не подойдет.
a∈
Как-то так. Если в задаче необходимо объединить решения пункта 1 и пункта 2, то ответ будет выглядеть так: a∈
Вообще, исходя из определений, критическая точка для функции одного переменного - это точка, в которой производная функции равна 0.
Далее, для пункта 1 нам нужно, чтобы исходная функция убывала на (-∞;+∞), для этого производная должна быть неположительной на этом же интервале и в одной точке должна быть равной нулю.
График производной - парабола (за исключением одного случая), причем её направление зависит от выражения с параметром. Нам нужно, чтобы парабола в одной точке касалась оси ОХ, а вся остальная парабола находилась ниже оси ОХ. То есть, её ветви должны быть направлены вниз.
Но для начала рассмотрим тот случай, когда a=-1 и это не парабола.
Вернемся к параболе. Направление ветвей вниз - ограничение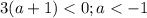
Условие, когда один корень - D=0 в уравнении y'=0
Тогда имеем два значения a: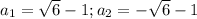
Учитывая ограничение a<-1 (корень из 6 больше 2), берем только a2.
Теперь к пункту 2, когда критических точек нет. На самом деле, всю работу мы почти сделали. Ещё раз выпишем производную
Теперь нам надо, чтобы даже касаний оси ОХ этой параболой не было. Тогда получается необходимость отсутствия корней уравнения y'=0. Этот случай при D<0 (корней нет, а сама парабола находится ниже оси ОХ, главное будет потом учесть ограничение на направление ветвей вниз - a<-1)
Чтобы решить это неравенство, нужно исследовать D как функцию, найти её нули и методом интервалов решить неравенство. Но нули её мы как раз нашли. Это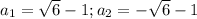
Методом интервалов получим левый крайний и правый крайний промежуток a∈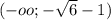 ∪
∪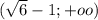
Но теперь надо учесть ограничение a<-1. Тогда правый промежуток нам не подойдет.
a∈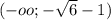
Как-то так. Если в задаче необходимо объединить решения пункта 1 и пункта 2, то ответ будет выглядеть так: a∈![(-oo;-\sqrt{6}-1]](/tpl/images/0712/5939/11cd4.png)