В точке х₁ = 0 производная меняет знак с - на +, поэтому х₁ = 0 - точка минимума.
В точке х₂ = -5 производная меняет знак с + на -, поэтому х₂ = -5 - точка максимума.
В интервале х ∈ [-6; 1] находятся и точка максимума х₂ = -5 и точка минимума х₁ = 0 , поэтому наибольшее значение функция будет иметь в точке х₂ = -5, а наименьшее значение а точке х₁ = 0
Наименьшее - 8
Наибольшее 10
Просто нужно представить 0 и - 6
у наиб = у(-5) = 12
у наим = у(0) = -8
Объяснение:
Функция
Производная функции
y' = x² + 5x
Найдём точки экстремумов
x² + 5x = 0
х(х + 5) = 0
х₁ = 0; х₂ = -5;
В точке х₁ = 0 производная меняет знак с - на +, поэтому х₁ = 0 - точка минимума.
В точке х₂ = -5 производная меняет знак с + на -, поэтому х₂ = -5 - точка максимума.
В интервале х ∈ [-6; 1] находятся и точка максимума х₂ = -5 и точка минимума х₁ = 0 , поэтому наибольшее значение функция будет иметь в точке х₂ = -5, а наименьшее значение а точке х₁ = 0
у наиб = у(-5) = (-5)³/3 + 5 · (-5)²/2 - 8 = -41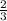 + 62,5 - 8 = 12
+ 62,5 - 8 = 12
у наим = у(0) = -8