Составить уравнение плоскости, проходящей через прямые (x−1)/3=(y+2)/2=(z−5(/(-2) и
⎪x=7+2t
⎨y=2−3t
⎪z=1+4t
Написать уравнение плоскости, проходящей через две заданные прямые можно, если эти прямые параллельны или пересекающиеся.
Нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки.
Уравнение первой прямой представим в параметрическом виде.
(x−1)/3=(y+2)/2=(z−5)/(−2) = a.
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
По непропорциональным коэффициентам параметров видно что прямые не параллельны.
Найдём точку пересечения прямых
x = 2t + 7,
y = -3t + 2,
z = 4t + 1,
и
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
Приравняем параметрические значения при одинаковых переменных.
2t + 7 = 3a + 1,
-3t + 2 = 2a – 2,
4t + 1 = -2a + 5.
=>
2t = 3a – 6,
-3t = 2a – 4,
4t = -2a + 4.
Приравняем правые части первого уравнения, умноженное на 2, и третье уравнение.
6a – 12 = -2a + 4,
8a = 16,
a = 16/8 = 2.
Подставим полученное значение а = 2 в параметрические уравнения второй прямой.
x = 3*2 + 1 = 7,
y = 2*2 – 2 = 2,
z = -2*2 + 5 = 1.
Найдём значение t по параметру а = 2.
2t = 3*2 – 6 = 0, t = 0,
-3t = 2*2 – 4 = 0, t = 0,
4t = -2*2 + 4 = 0, t = 0.
Подставим полученное значение t = 0 в параметрические уравнения первой прямой.
x = 2*0 + 7 = 7,
y = -3*0 + 2 = 2,
z = 4*0 + 1 = 1.
Значения перменных совпадают, значит, прямые пересекаются и найдена точка С их пересечения С(7; 2; 1).
Далее из уравнений прямых находим координаты не общих точек.
Из уравнения первой прямой (x−1)/3=(y+2)/2=(z−5)/(−2) определяем точку
1) x = ±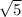
2) y =±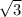
3) z = ±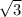
4) k = ±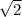
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±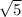
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
Обратная замена
y^2 = 3
y = ±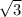
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =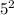
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
Обратная замена
z^2 = 3
z = ±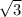
4) x^4 - 10x^2 + 9 = 0
Замена x^2 = t >0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
Обратная замена
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
Обратная замена
k^2 = 2
k = ±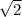
6) 49y^4 - 48y^2 - 1 = 0
Замена y^2 = t >0
49t^2 - 48t - 1 = 0
т.к. a + b + c = 0
t1 = 1
t2 = -1 - посторонний
Обратная замена
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
т.к. a + b + c = 0
x1 = 1
x2 = 4
Обратная замена
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
Замена x^2 = t >0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
Обратная замена
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
Составить уравнение плоскости, проходящей через прямые (x−1)/3=(y+2)/2=(z−5(/(-2) и
⎪x=7+2t
⎨y=2−3t
⎪z=1+4t
Написать уравнение плоскости, проходящей через две заданные прямые можно, если эти прямые параллельны или пересекающиеся.
Нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки.
Уравнение первой прямой представим в параметрическом виде.
(x−1)/3=(y+2)/2=(z−5)/(−2) = a.
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
По непропорциональным коэффициентам параметров видно что прямые не параллельны.
Найдём точку пересечения прямых
x = 2t + 7,
y = -3t + 2,
z = 4t + 1,
и
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
Приравняем параметрические значения при одинаковых переменных.
2t + 7 = 3a + 1,
-3t + 2 = 2a – 2,
4t + 1 = -2a + 5.
=>
2t = 3a – 6,
-3t = 2a – 4,
4t = -2a + 4.
Приравняем правые части первого уравнения, умноженное на 2, и третье уравнение.
6a – 12 = -2a + 4,
8a = 16,
a = 16/8 = 2.
Подставим полученное значение а = 2 в параметрические уравнения второй прямой.
x = 3*2 + 1 = 7,
y = 2*2 – 2 = 2,
z = -2*2 + 5 = 1.
Найдём значение t по параметру а = 2.
2t = 3*2 – 6 = 0, t = 0,
-3t = 2*2 – 4 = 0, t = 0,
4t = -2*2 + 4 = 0, t = 0.
Подставим полученное значение t = 0 в параметрические уравнения первой прямой.
x = 2*0 + 7 = 7,
y = -3*0 + 2 = 2,
z = 4*0 + 1 = 1.
Значения перменных совпадают, значит, прямые пересекаются и найдена точка С их пересечения С(7; 2; 1).
Далее из уравнений прямых находим координаты не общих точек.
Из уравнения первой прямой (x−1)/3=(y+2)/2=(z−5)/(−2) определяем точку
А(1; -2; 5).
Найдём точку B на второй прямой, подставив t = 1.
x = 2*1 + 7 = 9,
y = -3*1 + 2 = -1,
z = 4*1 + 1 = 5.
Найдена точка В(9; -1; 5).
По трём точкам А(1; -2; 5), В(9; -1; 5), С(7; 2; 1).составляем уравнение плоскости.
Находим векторы АB и АC.
Вектор АВ = (9-1; -1-(-2); 5-5) = (8; 1; 0).
Вектор АC = (7-1; 2-(-2); 1-5) = (6; 4; -4).
Нормальный вектор плоскости АBC находим из векторного произведения векторов АB и АC.
i j k| i j
8 1 0| 8 1
6 4 -4| 6 4 = -4i + 0j + 32k + 32j - 0i - 6k =
= -4i + 32j + 26k.
Нормальный вектор плоскости АBC равен (-4; 32; 26).
Примем коллинеарный ему вектор с к = -2: (2; -16; -13)
Уравнение плоскости, проходящей через точку Mo(xo;yo;zo), с нормальным вектором n=(A;B;C) имеет вид A·(x–xo)+B·(y–yo)+C·(z–zo)=0.
Подставим данные: А(1; -2; 5), n = (2; -16; -13).
2·(x – 1) + (-16)· (y + 2) + (-13)·(z - 5) = 0.
2x - 2 - 16y - 32 - 13z + 65 = 0.
2х - 16y - 13z + 31=0.
О т в е т. 2х - 16y - 13z + 31 = 0.