Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
Леееера1
21.06.2021 23:48 •
Алгебра
упростить и вычислить
если
Показать ответ
Ответ:
Vostafi
19.03.2022 12:50
При
:
ответ: 2
0,0
(0 оценок)
Популярные вопросы: Алгебра
foxmanlp
18.01.2023 06:45
Y = x cos 2х четная или нечетная функция?...
evgen22regiooon
12.10.2021 05:03
Надо Периметр прямоугольника 80 см. Какими должны бытьего длина и ширина. Чторы Плошадь прямоугольника была наибольшей?...
SilvAqualius
07.10.2020 18:12
решить карточку по алгебра...
Jasurka940
01.09.2020 23:32
Перегон в 60 км поезд должен был проехать с постоянной скоростью за определенное расписанием время у семафора перед перегоном 5 минут, машинист вынужден был увеличить...
лауракот
27.07.2022 08:53
7/10×x+1/5×x=1×19/20-1/5×x...
BrainSto
18.11.2021 07:09
Это графики,объясните как это вообще делать?...
AlionaCeban
19.06.2020 23:52
Расположить в порядке убывания числа √3; 3 √4; 6 √18...
Неко6тян
18.02.2023 05:35
Ширина прямоугольника на 3 см меньше его длины.найдите ширину прямоугольника ,если его площадь равна 130 см^2...
Vankoed
26.05.2020 14:00
Выражение : 1)a³*(a²)⁴; 2)(a²)⁴*(a⁴)³; 3)(p²*p³)²; 4)(m²*m³)³; 5)(x²)⁵*x⁵; 6)(y²*y³)⁴...
Operator404
23.12.2020 00:38
На доске написано число 321321321321 .какие цифры надо убрать чтобы получить возможное наибольшее число ,делящеесяна 9...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
При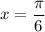 :
:
ответ: 2