Рассматривается выражение
Докажем, что y положительно при любом значении x. Допустим, что это не так. Найдём такие x, при которых y ≤ 0. Для этого решим неравенство:
Или
Что не имеет решений, так как
Мы пришли к противоречию. Следовательно, принимает положительное значение при любых x.
Для нахождения наименьшего значения найдём :
Приравняв его 0, найдём точку экстремума:
Убедимся, что найденная точка — действительно минимум.
Итак, первая производная меняет в точке знак с "-" на "+", следовательно, в этой точке мы действительно имеем минимум.
Значение y при x = -4:
Рассматривается выражение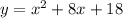
Докажем, что y положительно при любом значении x. Допустим, что это не так. Найдём такие x, при которых y ≤ 0. Для этого решим неравенство:
Или
Что не имеет решений, так как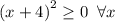
Мы пришли к противоречию. Следовательно,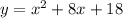
принимает положительное значение при любых x.
Для нахождения наименьшего значения найдём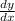
:
Приравняв его 0, найдём точку экстремума:
Убедимся, что найденная точка — действительно минимум.
Итак, первая производная меняет в точке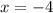
знак с "-" на "+", следовательно, в этой точке мы действительно имеем минимум.
Значение y при x = -4:
9x^2+12x+4=10+3x^2+6x-6x-12
9x^2+12x+4-10-3x^2-6x+6x+12=0
6x^2+12x+6=0
D=12^2−4·6·6=144−144=0(Уравнение имеет один корень)
X1=-12/2*6=-12/12=-1
2)4x^2-12x+9=9-2(x^2+3x-3x-9)
4x^2-12x+9=9-2x^2-6x+6x+18
4x^2-12x+9-9+2x^2+6x-6x-18=0
6x^2-12x-18=0
D=(−12)^2−4·6·(−18)=144+432=576=24
x1=-(-12)+24/2*6=36/12=3
X2=-(-12)-24/2*6=-12/12=-1
3)x^3-2x^2+4x+2x^2-4x+8-x^3-2x^2=0
-2x^2+8=0
2x^2-8=0
D=0^2−4·2·(−8)=0+64=64=8
x1=-0+8/2*2=8/4=2
x2=-0-8/2*2=-8/4=-2
4)x^3+x^2-x-x^2-x+1-x^3+x^2=0
x^2-2x+1=0
D=(−2)^2−4·1·1=4−4=0 (Уравнение имеет один корень)
x1=-(-2)/2*1=2/2=1