Упростите выражение: ( y²/x³-xy²+1/x+y): (x-y/x²+xy- x/xy+y²​)
(a/a-4-a/a+4-a²+16/16-a²):4a+a²/(4-a)²

Допустим 1/(3√2):  1/(3√2)-4+1/(3√2)+4=2/(3√2)
9)(1/1+√2+1/1-√2)*(4-2√2)=(1/(1+√2)+1/(1-√2))*(4-2√2)=((1-√2+1+√2)/(1-(√2)²)*(4-2√2)=2/(-1)*(4-2√2)=-8+4√2=4√2-8
10)избавиться от иррационала
7-4√3/√3-2=(7-4√3)/(√3-2)=((7-4√3)*(√3+2))/((√3-2)/(√3+2))=(7√3+14-12-8√3)/(3-4)=(2-√3)/(-1)=-(2-√3)=√3-2
11)√20.25+0.5*√12-5/6-1/2*√12+27*√1/81
12)1/7-√39-1/7+√39=0
13)√√17-1*√√17+1=(√(√17-1))*(√(√17+1))=√((√17-1)(√17+1))=√(17-1)=√16=4
√√67-√19*√√67+√19=(√(√67-√19))*(√(√67+√19))=√((√67-√19)(√67+√19))=√(67-19)=√48=4√3
∛√52-5*∛√52+5
√7/√7+√3+√3/√7-√3=√7/(√7+√3)+√3/(√7-√3)=(√7*(√7-√3)+√3(√7+√3)) / (7-3)=
(7-√21+√21+3) / 4=10/4=5/2=2,5
√27+10√2+√27-10√2=2√27=2*3√3=6√3

Кусочная функция  на графике  нарисована сплошными линиями .

Рисуем параболу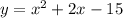     при изменении переменной "х" в пределах от  -3 до 3 ,  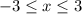  .  Ветви параболы направлены вверх, вершина параболы в точке (-1;-16) . Точки (3;0)  и (-3;-12) принадлежат графику .

Прямую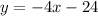     рисуем при  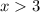  . Точка (3;0) не принадлежит графику .

Прямую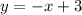     рисуем при  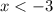  .  Точка (-3;-12) не принадле-жит графику .

  при    .

б)  область значений функции:    ,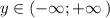

    при   х=5  значение функции  у=-2  ,    .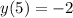

в)   пересечение с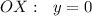     при    ,    .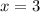

     пересечение с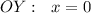    ,  если    .

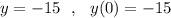г)  y(x) возрастает при    .

    y(x) убывает при    ,