Відомо що D(f) = [-5;2] знайдіть область визначення функції y = f (x-3)

Находим корни уравнения    .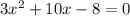

Дальше можно : либо методом интервалов, либо начертив параболу (схематично) .

1)  Метод интервалов.

Раскладываем квадратный трёхчлен на множители.

На числовой оси отмечаем нули функции (то есть корни кв. трёхчлена) . Вычисляем знаки на каждом интервале. Нас интересует знак (+), так как знак неравенства  " ≥ " .

Знаки:    

ответ:    

2)   Начертим схематично параболу, учитывая, что ветви её направлены вверх, так как коэффициент при  х²  равен 3>0 .

И посмотрим, на каких промежутках график лежит выше оси ОХ .

В обоих случаях учитываем , что знак неравенства не строгий, а поэтому корни (нули функции) входят в нужные промежутки .

См. рисунок.

ответ:    .

Объяснение:

Задание 1

а) 5, 10, 15,...; - возрастающая арифметическая прогрессия (d = 5).

б) 3, 0, - 3,...; - убывающая арифметическая прогрессия (d = -3).

г) - 6, - 4, - 2,...; - возрастающая арифметическая прогрессия (d = 2).

д) 11, 9, 7,...; - убывающая арифметическая прогрессия (d = -2).

в) 7, 12, 17,...; - возрастающая арифметическая прогрессия (d = 5).

Задание 2.

d = 2;

a1 = 3, тогда прогрессия такова:

3; 5; 7; 9; 11.

Задание 3.

а) 1, 1, 1, 1, 1, 1, ...;

б) 5, 3, 1, - 1, - 3, - 5, ...

в) - 2, 2, 6, 10, 14, 18,...