пусть скорость плота х км/ч,учитываем,что скорость плота равна скорости течения реки,тогда по течению скорость лодки равна (8 + х) км/ч, а против течения (8 - х) км/ч.
составим уравнение:
15/(8+x)+ 6/(8-x)=5/x;
(120-15х+48+6х)/(64+х²)=5/x;
(168-9x)/(64+x²)-5/x=0;
(168x-9x²-320+5x²)/(64х+х³)=0;
168x-9x²-320+5x²=0;
-4x²+168x-320=0;
сокращаем на -4:
x²-42x+80=0;
d=b²-4×a×c
d=(-42²)-4×1×80 = 1764-320=1444
d> 0, 2 корня
х₁=42+√1444/2×1 =42+38/2=80/2=40 (км/ч)---не подходит(так как плот не может плыть быстрее лодки, значит х=40 не является решением);
х₂=42-√1444/2×1=42-38/2=4/2=2 -(км/ч)---скорость течения реки;
ответ:
ответ: 2 км/ч.
объяснение:
решение:
пусть скорость плота х км/ч,учитываем,что скорость плота равна скорости течения реки,тогда по течению скорость лодки равна (8 + х) км/ч, а против течения (8 - х) км/ч.
составим уравнение:
15/(8+x)+ 6/(8-x)=5/x;
(120-15х+48+6х)/(64+х²)=5/x;
(168-9x)/(64+x²)-5/x=0;
(168x-9x²-320+5x²)/(64х+х³)=0;
168x-9x²-320+5x²=0;
-4x²+168x-320=0;
сокращаем на -4:
x²-42x+80=0;
d=b²-4×a×c
d=(-42²)-4×1×80 = 1764-320=1444
d> 0, 2 корня
х₁=42+√1444/2×1 =42+38/2=80/2=40 (км/ч)---не подходит(так как плот не может плыть быстрее лодки, значит х=40 не является решением);
х₂=42-√1444/2×1=42-38/2=4/2=2 -(км/ч)---скорость течения реки;
ответ: 2 км/ч.
Объяснение:
1) а) В уравнении один корень когда модуль равен 0, а он принимает это значение при а=-3
б) уравнение не имеет корней, когда модуль равен отрицательному числу, то есть число а лежит в интервале (-2;2)
2) х=-2/а
х=3/(а+2)
х=(а-3)/(а-3)=-1
3) a)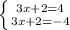
значит либо 3х=2, то есть х=2/3, либо 3х=-6, то есть х=-2
б) так как модуль больше нуля при любых х, то корней нет, так как он равен -2
в) x^2+x=0 ⇒ x(x+1)=0⇒ x1=0; x2=-1
г) 1.|x+3|-4=1 или |x+3|-4=-1
|x+3|=5 или |x+3|=3
х+3=5 или х+3=-5 или х+3 =3 или х+3=-3
х=2 или х=-8 или х=0 или х=-6