Объём V тела (но не фигуры) равен объёму V1 тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции у = х^3 минус объём V2 конуса, направляющая которого - это касательная к графику кривой.
Объём конуса
Решение:
Высота конуса Н = 1/3 определена по разности х = 1 (граница фигуры на графике) и х =(2/3) как точка пересечения касательной оси Ох.
Дана система уравнений :
{х+ Зу = 5, это прямая линия у = (-1/3)х + (5/3)
{х² + y² = 25, это окружность с центром в начале координат и радиусом 5.
Общая схема графического решения - начертить окружность и провести линию через 2 точки: х = 0, у = (5/3) и у = 0, х = 5.
Точки пересечения линий и есть решение.
Можно аналитически проверить его правильность.
{х+ Зу = 5, х = 5 - 3у подставить во второе уравнение.
{х² +y² = 25. (5 - 3у)² + у² = 25.
25 - 30у + 9у² + у² = 25. Решаем квадратное уравнение:
10у² - 30у = 0 или 10у(у - 3) = 0.
Получили 2 корня: у1 = 0 и у2 = 3, отсюда соответствующие координаты по оси Ох равны:
х1 = 5, х2 = -4.
Объём V тела (но не фигуры) равен объёму V1 тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции у = х^3 минус объём V2 конуса, направляющая которого - это касательная к графику кривой.
Объём конуса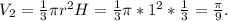
Решение: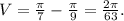
Высота конуса Н = 1/3 определена по разности х = 1 (граница фигуры на графике) и х =(2/3) как точка пересечения касательной оси Ох.
Уравнение касательной у(кас) = y'(x - xo) + yo.
y' = 3x², y'(1) = 3,
y(1) = 1³ = 1.
Уравнение касательной: у = 3(х - 1) + 1 = 3х - 3 + 1 = 3х -2.
Отсюда при у = 0 получаем х = (2/3).