Вдороге туда турист провёл на 2 часа меньше , чем обратно , потому что на обратном пути снизил скорость от 6 км/ч до 4 км/ч . сколько км он совершил ? уравнение для решения этой является , в частности ,

Показать ответ

Ответ:

Abdueva

07.09.2020 01:42

Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.

1-ое свойство, которое понадобится

$a+c \equiv b + d \ (mod \ m)$

То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.

2-ое свойство, которое нам понадобится:

$ac \equiv bd \ (mod \ m)$

То есть довольно аналогичная вещь в произведении

На нашем примере все увидим

$a = 5\cdot 2^{51}+21\cdot 32^{45}$

Находим остатки по модулю 31

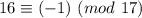Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, $16 \equiv (-1) \ (mod \ 17)$ , но сейчас это не нужно), нам повезло, это 32

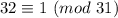Учитываем, что $32 \equiv 1 \ (mod \ 31)$ , получаем

$5\cdot 2^{51} = 5\cdot 2^1 \cdot 2^{50}=10 \cdot 2^{10\cdot 5} = 10 \cdot (2^{5})^{10}= 10\cdot 32^{10} \equiv 10 \cdot 1^{10} \ (mod \ 31)$

То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым

$21\cdot 32^{45} \equiv 21 \cdot 1^{45}\ (mod \ 31) \equiv 21 \ (mod \ 31)$

Остаток 21, чудесно. Выполняем последний шаг.

$5\cdot 2^{51}+21\cdot 32^{45} \equiv 10+21 \ (mod \ 31) \equiv 31 \ (mod \ 31) \equiv 0 \ (mod \ 31)$

То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.

0,0(0 оценок)

Ответ:

Aprengreid

20.07.2022 14:20

ответ: 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).

Объяснение:

Запишем данный многочлен в виде 2*(x³+5/2*x²+1/2*x-1). Для того, чтобы разложить многочлен в скобках на множители, нужно решить уравнение x³+5/2*x²+1/2*x-1=0. Это - приведённое кубическое уравнение, поэтому одним из его целых корней (если они есть) может быть целый делитель свободного члена данного уравнения, то есть числа -1. Таких делителей всего два: 1 и -1. Подставляя значения x=1 и x=-1 в данное уравнение, находим, что число x=1 не является корнем уравнения, а число x=-1 - является. Теперь разделим многочлен x³+5/2*x²+1/2*x-1 на двучлен x-(-1)=x+1. После этого получим тождество x³+5/2*x²+1/2*x-1=(x+1)*(x²+3/2*x-1). Теперь разложим на множители квадратный трёхчлен x²+3/2*x-1, для чего нужно решить уравнение x²+3/2*x-1=0. Оно имеет корни x1=1/2 и x2=-2, поэтому x²+3/2*x-1=0=(x-1/2)*(x+2). Тогда x³+5/2*x²+1/2*x-1=(x+1)*(x-1/2)*(x+2) и окончательно 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).

0,0(0 оценок)

Популярные вопросы: Алгебра