Переформулируем условие в терминах арифметической прогрессии:
1) В первый день потратили 100 рублей = первый член прогрессии равен 100.
2) Каждый последующий день тратили на 50 рублей больше = разность прогрессии равна 50.
3) Всего было 1000 рублей = сумма членов (то есть дней) равна 1000.
Сумма вычисляется по формуле
Чтобы найти , подставим в эту формулу известные числа:
Решим это уравнение с дискриминанта:
Количество дней не может быть отрицательным, поэтому имеем единственный ответ:
ответ: на пять дней.
Замена : х^2 +2х -3=у
Получим:
24 / у -5 - 15 / у =2
24у - 15( у-5) =2у(у-5)
24у -15у + 75 = 2у^2 - 10у
- 2у^2 +19 у +75=0 ( * -1)
2у^2 -19у-75=0
Д= корень из 961 =31
У1= 19+31 /4 =12,5
У2=19-31. /4= - 3
Х^2 +2х-3=у1
Х^2+2х-3=12,5
Х^2+2х-15,5 =0
Д=корень из 64=8
Х1=-2+8 / 2= 3
Х2= - 2 - 10. / 2 = - 6
Х^2 +2х - 3 = у2
Х^2 +2х -3= -3
Х^2 +2х =0
Х(Х+2)=0
Х3=0
Х+2=0
Х4= - 2
Точно так же в последнем примере делаем замену:
Х^2 -2х+2=у
В 1-й дроби будет знаменатель у
Во 2-й дроби (у+1)
В 3-ей дроби (у+2)
1/у + 2 / у+1 = 6 / у+2
Переформулируем условие в терминах арифметической прогрессии:
1) В первый день потратили 100 рублей = первый член прогрессии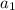 равен 100.
равен 100.
2) Каждый последующий день тратили на 50 рублей больше = разность прогрессии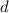 равна 50.
равна 50.
3) Всего было 1000 рублей = сумма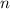 членов (то есть
членов (то есть 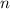 дней) равна 1000.
дней) равна 1000.
Сумма вычисляется по формуле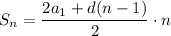
Чтобы найти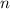 , подставим в эту формулу известные числа:
, подставим в эту формулу известные числа:
Решим это уравнение с дискриминанта:
Количество дней не может быть отрицательным, поэтому имеем единственный ответ: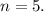
ответ: на пять дней.