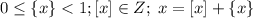Витративши половину всіх коштів, учень побачив, що гривень в нього залишилось вдвічі менше, ніж спочатку було копійок і стільки копійок, скільки на початку було гривенью скільки грошей витратив учень, якщо копійок в нього було менще ніж, сто?
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение
2)
А значит, если взять (*), . И правда:
(*) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)
А значит, если взять (**), . И правда:
(**) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.
Тут нужно решать интервальным методом, показать здесь я это не могу. Но для начала нужно найти нули функции(значения х, при котором функция была бы равна нулю). Здесь нули ф.: 4;-3,5. Затем чертим ось ох, обозначаем эти точки и участки, где функция положительна или отрицательна. В итоге получаем, что функция <0 при х принадлежащем отрезку (-3,5;4) 2 решается точно так же, но тут для удобства нужно в 1 скобуе поменять местами числа, затем вынести за скобки -1 и умножить обе части неравенства на -1(при этом знак> меняется на знак <). Вот что получается (х-2)(х+1)<0. Нули функции: 2;-1. Дальше как я уже объяснял выше. ответ: при х принадлежащем отрезку (-1;2)
По определению,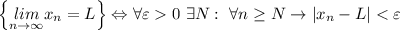
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение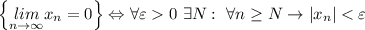
2)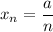
А значит, если взять![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*), 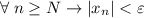 . И правда:
. И правда: 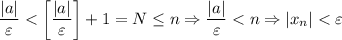
(*) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)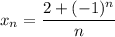
А значит, если взять![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**), 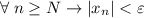 . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда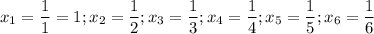
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.