(x²-ax +1)/(x+3)=0 ОДЗ x≠-3 1. D=a²-4=0 a=2 , x²-2x +1=0 x=1 одно решение a=-2, x²+2x +1=0 x=-1 одно решение 2. D=a²-4 >0, и один корень равен -3: a∈(-∞;-2)∪(2;∞) х₀-3=a -3x₀=1 ⇔ при a=-3-1/3 x=-1/3 одно решение
4) При каких a неравенство 2x-a>0 является следствием неравенства x+2a-3>0
2x-a>0 x>a/2 - + (a/2).....---.
x+2a-3>0 x>-2a+3 - + (-2a+3)..---.---.....---
неравенство 2x-a>0 является следствием неравенства x+2a-3>0 другими словами x∈(a/2;∞)⊆x∈(-2a+3;∞)⇔(-2a+3)≤a/2 ⇔2,5a≥3 ⇔2,5a≥3 ⇔ a≥6/6
x+5=0 x=-5 - + +
(-5)
2x-3=0 x=1,5 + + -
(1,5)
-(x+5)+(-2x+3)=3 при x∈(-∞,-5) -3x=5 x=-5/3 x∉(-∞,-5)
(x+5)+(-2x+3)=3 при x∈(-5;1,5) -x+8=3 x=5 x∉(-5;1,5)
(x+5)-(-2x+3)=3 при x∈(1,5;∞) 3x=1 x=1/3 ∉ (1,5;∞)
нет решений
2)Решите неравенство
Ix²-6x I >7
1. x²-6x >7 ∪ 2. x²-6x < -7
+ - +
1. x²-6x -7 >0 ⇔ (-1)(7)
x∈(-∞;-1)∪ (7;∞)
+ - +
2. x²-6x +7< 0 (3-√2)(3-√2)x∈(3-√2;3-√2)
ответ: x∈(-∞;-1)∪(3-√2;3-√2)∪ (7;∞)
3)При каких значениях a уравнение имеет единственное решение?
(x²-ax +1)/(x+3)=0 ОДЗ x≠-3
1. D=a²-4=0 a=2 , x²-2x +1=0 x=1 одно решение
a=-2, x²+2x +1=0 x=-1 одно решение
2. D=a²-4 >0, и один корень равен -3:
a∈(-∞;-2)∪(2;∞) х₀-3=a
-3x₀=1 ⇔ при a=-3-1/3 x=-1/3 одно решение
4) При каких a неравенство 2x-a>0 является следствием неравенства x+2a-3>0
2x-a>0 x>a/2
- +
(a/2).....---.
x+2a-3>0 x>-2a+3
- +
(-2a+3)..---.---.....---
неравенство 2x-a>0 является следствием неравенства x+2a-3>0
другими словами x∈(a/2;∞)⊆x∈(-2a+3;∞)⇔(-2a+3)≤a/2 ⇔2,5a≥3
⇔2,5a≥3 ⇔ a≥6/6
Объяснение:
Пример №1.
Для решения данного уравнения надо вспомнить 6 свойство числовых неравенств, которое изучается по алгебре в 8 классе:
если произведение чисел равно нулю, то это значит, что один из множителей равен нулю.
То есть, мы приравниваем все скобки к нулю.
Приравниваем:
2x - 3 = 0
x + 1 = 0
3 - x = 0
Решаем линейные уравнения(Перенос чисел без переменной вправо с изменением знака на противоположный, а также деление на коэффициент при переменной).
x = 1`,5
x = -1
x = 3
Пример №2.
Уравнение, у которого первый коэффициент имеет четвертую степень, называется биквадратным.
Пусть x^2 - это t, а t положительно.
Тогда получим уравнение:
t^2 + 3t = 0
Решим квадратное уравнение: для этого t вынесем за скобку.
Получим:
t(t + 3) = 0
Если произведение двух чисел равно нулю, то один из множителей также равен нулю.
t = 0
t + 3 = 0
Откуда t = 0; t = -3
Но t - это икс в квадрате. То есть, нам надо извлечь корень квадратный из полученных результатов.
x^2 =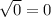
x^2 =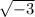 - по условию не подходит, т.к. корень квадратный извлекать из чисел, меньших нуля, нельзя.
- по условию не подходит, т.к. корень квадратный извлекать из чисел, меньших нуля, нельзя.
Задача решена. Если есть вопросы - задавай.