1) f(x)=1.2x-10
Линейная функция
область определения R
область значений R
растёт на промежутке (-∞ ; +∞)
не парная не непарная
не переиодичная
точки пересечения с осями
ОХ: 1,2х-10=0
1,2х=10
х=100/12= 8 1/3
ОУ: 1,2*0-10 = -10
Построим по таблице функцию f(x) = 1.2x и паралельным переносом перенесем по оси ординат на 10 единиц вниз (рисунок 1)
2) 3x^2-7x
Квадратическая функция, графиком которой является парабола
Область определения R
функция ни четная ни нечетная
Область значений y є [ ; + ∞)
Ветки вверх , т.к. a больше нуля
Найдем координаты вершины параболы
x0 = -(-7) / 2*3 ≈ 1.1
y0 = 3 * - 7* = 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
С ОХ 3х^2-7x=0
x(3x-7)=0
x1 = 0
x2 = 7/3
С ОУ 3*0^2 - 7*0 = 0
Строим график по данным (рисунок 2)
<=; =>; =<; >=; - меньше/больше или равно
1) 84х - 20 <= 80х + 20
4х <= 40
х <= 10
2) 3,4х + 11х + 7 < 34х + 0.4х + 8
14,4х + 7 < 34,4х + 8
20х > -1
х > -0.05
3) 0х > 0
0 > 0
нет решения
4) 0х >=5
0 >=5
5) 28х <= 14
х <= 0.5
1) 14 <= (х + 8)/3 - 1 <= 33 | ×3
42 <= х+8 - 3 <= 99 | -5
37 <= х <= 94
2) 0 <= (3х - 8)/2 + 4 <= 2 | ×2
0 <= 3х - 8 + 8 <= 4 | ÷3
0 <= х <= 4/3
3) 17 <= (4 - 2х)/3 + 1 <= 5 |
решения нет, тк нет числа, которое больше 17 но меньше 5
4) 2 <= ((8 - 11х)/2 - 1) × 1/3 <= 7 | ×3
6 <= (8 - 11х)/2 - 1 <= 21 | ×2
12 <= 8 - 11х - 2 <= 42 | -6
6 <= -11х <= 36 | ÷(-11) (знаки переворачиваются)
-36/11 <= х <= -6/11
1) 11х/4 > 3/8 | ×8
22х > 3
х > 3/22
2) 2х/3 <= 1 | ×3
2х <= 3
х <= 1.5
3) 17х/17 > 0 | ×17
17х > 0
х > 0
1) f(x)=1.2x-10
Линейная функция
область определения R
область значений R
растёт на промежутке (-∞ ; +∞)
не парная не непарная
не переиодичная
точки пересечения с осями
ОХ: 1,2х-10=0
1,2х=10
х=100/12= 8 1/3
ОУ: 1,2*0-10 = -10
Построим по таблице функцию f(x) = 1.2x и паралельным переносом перенесем по оси ординат на 10 единиц вниз (рисунок 1)
2) 3x^2-7x
Квадратическая функция, графиком которой является парабола
Область определения R
функция ни четная ни нечетная
Область значений y є [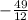 ; + ∞)
; + ∞)
Ветки вверх , т.к. a больше нуля
Найдем координаты вершины параболы
x0 = -(-7) / 2*3 ≈ 1.1
y0 = 3 *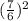 - 7*
- 7* 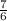 = 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
= 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
точки пересечения с осями
С ОХ 3х^2-7x=0
x(3x-7)=0
x1 = 0
x2 = 7/3
С ОУ 3*0^2 - 7*0 = 0
Строим график по данным (рисунок 2)
<=; =>; =<; >=; - меньше/больше или равно
1) 84х - 20 <= 80х + 20
4х <= 40
х <= 10
2) 3,4х + 11х + 7 < 34х + 0.4х + 8
14,4х + 7 < 34,4х + 8
20х > -1
х > -0.05
3) 0х > 0
0 > 0
нет решения
4) 0х >=5
0 >=5
нет решения
5) 28х <= 14
х <= 0.5
1) 14 <= (х + 8)/3 - 1 <= 33 | ×3
42 <= х+8 - 3 <= 99 | -5
37 <= х <= 94
2) 0 <= (3х - 8)/2 + 4 <= 2 | ×2
0 <= 3х - 8 + 8 <= 4 | ÷3
0 <= х <= 4/3
3) 17 <= (4 - 2х)/3 + 1 <= 5 |
решения нет, тк нет числа, которое больше 17 но меньше 5
4) 2 <= ((8 - 11х)/2 - 1) × 1/3 <= 7 | ×3
6 <= (8 - 11х)/2 - 1 <= 21 | ×2
12 <= 8 - 11х - 2 <= 42 | -6
6 <= -11х <= 36 | ÷(-11) (знаки переворачиваются)
-36/11 <= х <= -6/11
1) 11х/4 > 3/8 | ×8
22х > 3
х > 3/22
2) 2х/3 <= 1 | ×3
2х <= 3
х <= 1.5
3) 17х/17 > 0 | ×17
17х > 0
х > 0