Вычисли сумму первых 6 членов арифметической прогрессии (an), если даны первые члены: 1;7...

S6 =

Показать ответ

Ответ:

MrHezbollah

13.04.2021 02:05

Возьмем приближенно $\pi \approx3.14$

Рассмотрим число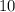 . На числовой окружности этому числу соответствует та же точка, что и числу $10-2\pi$ :

$10-2\pi\approx10-2\cdot3.14=3.72$

Зная, что $\pi \approx3.14$ и $\dfrac{3\pi}{2} \approx4.71$ , получаем, что число 3.72 располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.

Заметим, что число 3.72 располагается ближе к числу $\pi$ , так как $|3.72-\pi|$ .

Зарисуем схематично число в 3 четверти, расположенное ближе к числу $\pi$ . По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):

$\cos10$

Рассмотрим тангенс. Так как тангенс положительный, то заменим отношение синуса к косинусу отношением их модулей:

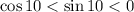$\mathrm{tg}10=\dfrac{\sin10}{\cos10} =\dfrac{|\sin10|}{|\cos10|}$

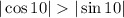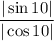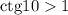Зная, что $\cos10$ , получим, что $|\cos10||\sin10|$ , соответственно дробь $\dfrac{|\sin10|}{|\cos10|}$ правильная, значит $\mathrm{tg}10$ . Тогда, так как котангенс есть величина, обратная тангенсу, то $\mathrm{ctg}101$ .

Итоговая цепочка: $\cos10$

0,0(0 оценок)

Ответ:

домашкидофига

19.12.2020 22:22

Имеем функцию:

y = x^2 - 6 * x - 13.

Найдем ее минимальное и максимальное значения на промежутке [-2; 7].

Порядок решения такой - для начала найдем критические точки функции, и затем сравним значения функции от критического аргумента и границ промежутка - этого будет достаточно.

Находим производную функции:

y' = 2 * x - 6;

y' = 0;

x = 3 - критическая функция. Находим значения функции:

y(-2) = 4 + 12 - 13 = 3;

y(3) = 9 - 18 - 13 = -22;

y(7) = 49 - 42 - 13 = -6.

Получаем, что:

Минимальное значение функции на промежутке - -22.

Максимальное значение функции на промежутке - 3.

0,0(0 оценок)

Популярные вопросы: Алгебра