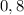Используем основное тригонометрическое тождество:
Откуда
Значение находится в пределах от до , что соответствует его расположению в первой координатной четверти, а функция косинус в первой координатной четверти положительна, поэтому:
ответ:
Используем основное тригонометрическое тождество: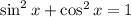
Откуда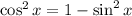
Значение находится в пределах от
находится в пределах от 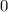 до
до 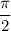 , что соответствует его расположению в первой координатной четверти, а функция косинус в первой координатной четверти положительна, поэтому:
, что соответствует его расположению в первой координатной четверти, а функция косинус в первой координатной четверти положительна, поэтому:
ответ: