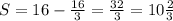Плошадь искомой фигуры - разность площадей примоугольника ограниченного у=4, осью х и перпендикулярями их точки пересечения (х1=-2, х2=2) и ограниченного кривой у=х^2, осью х и перпендикулярами в точках х1=-2, х2=2
Площадь прямоугольника. S=a*b, длина а=2+2=4 (по оси х), b=4 (по оси у)
1 находим точки пересечения кривых
Плошадь искомой фигуры - разность площадей примоугольника ограниченного у=4, осью х и перпендикулярями их точки пересечения (х1=-2, х2=2) и ограниченного кривой у=х^2, осью х и перпендикулярами в точках х1=-2, х2=2
Площадь прямоугольника. S=a*b, длина а=2+2=4 (по оси х), b=4 (по оси у)
S=4*4=16
2.площаль фигуры ограниченной у=х^2
3. находим разность